Enunciado
Física - Moysés - Vol. 2 - Ed: 4º - Capítulo 3.Problemas - Ex. 7
Um pêndulo balístico de madeira, de massa igual a , suspenso por um fio de de comprimento, é atingido no instante por uma bala de , viajando à velocidade de , que fica encravada nele. Ache o ângulo (em rad) entre o fio e a vertical como função de .
Passo 1
Vamos começar fazendo um desenho da situação antes e depois da colisão:
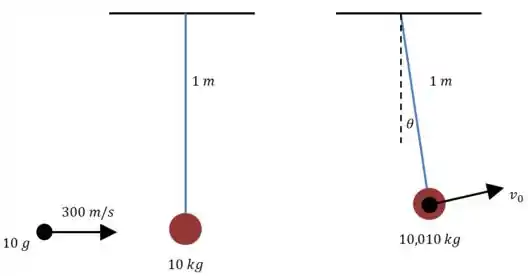
Vamos encontrar a velocidade usando a conservação de momento linear:
Beleza, essa é uma das condições iniciais que nós vamos usar para achar a função .
Passo 2
Agora vamos lembrar da fórmula geral para o ângulo de um pêndulo simples (que é simplesmente um oscilador harmônico):
Onde a frequência angular é:
Vimos que a velocidade inicial é , então:
Podemos derivar para encontrar :
E no instante :
Essa é nossa primeira condição inicial. Além disso, sabemos que a posição angular inicial é , então:
Vamos juntar as duas em um sistema:
Passo 3
Agora vamos resolver esse sistema para encontrar e . Pela primeira equação temos:
Substituindo isso na segunda:
Então:
E como :
Resposta
O ângulo entre o fio e a vertical é .