Enunciado
Física - Curso de Física Básica - Mecânica Volume 1 - 5ª Edição - Herch Moysés Nussenzveig- Ed: 5º - Capítulo 10.Problemas - Ex. 13
Calcule o campo gravitacional produzido por uma camada esférica homogênea de densidade , raio interno e raio externo , num ponto situado dentro da camada, à distância do centro (. Mostre que para uma camada delgada o campo varia linearmente (com boa aproximação) entre as superfícies interna e externa.
Passo 1
A gente está trabalhando com casca. A sua parte interna é oca, e então não tem massa, certo? Mas se não tem massa não tem campo gravitacional! Então a gente só precisa se preocupar com a massa que está entre o centro e .
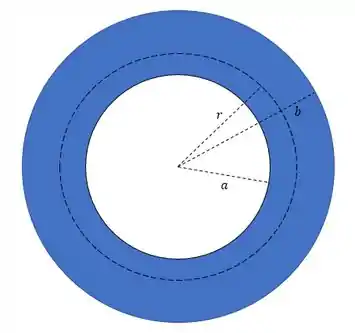
O campo a uma distância do centro é:
Passo 2
Agora precisamos achar a massa que está dentro dessa região, que pode ser calculada em função da densidade e do volume.
Não esquece que entre o centro e a borda de esfera de raio é tudo oco. Logo,
Portanto,
Passo 3
O volume entre o centro e a borda de esfera de raio será:
Assim,
Como já achamos a massa agora é só voltar pra expressão do campo!
Esse resultado que a gente encontrou não é exatamente linear, mas ele é quaaaase linear! Porque se a gente for escrever isso em função de , vai ficar assim:
O primeiro termo é linear, beleza, mas o segundo termo não é... Então a gente não pode dizer que é linear não. Mas pra um bem grande, é linear sim, porque esse fator fica beeem pequeno!