Considere os seguintes objetos oscilado num plano vertical: aro circular de diâmetro l , suspenso de O a e placa circular homogênea de diâmetro l suspensa de O b . Compare os respsectivos períodos τ a e τ b com o período de oscilação τ de um pêndulo simples de comprimento l .

(a) τ a = τ .(b) τ b = 3 2 τ .

Enunciado

(a) O aro circular está oscilando em torno do ponto . A única força que produz torque em torno desse ponto é o peso do aro:

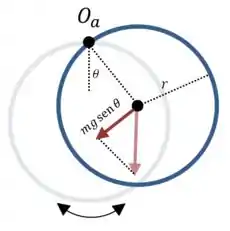
E a componente da força peso está agindo a uma distância do centro de rotação:

O sinal negativo aparece porque o peso age para diminuir o ângulo .

Agora precisamos calcular o momento de inércia do aro em relação ao ponto .

Nós já conhecemos o momento de inércia em relação ao centro, então só precisamos usar o teorema dos eixos paralelos:

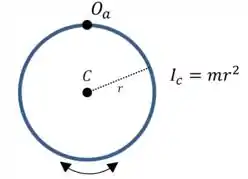
Onde é a distância entre e :

Substituindo na equação de cima:

Dividindo por e aproximando , ficamos com o seguinte:

Como , temos:

Que é a equação de um oscilador harmônico com a seguinte frequência angular:

E o seguinte período:

Que é exatamente o mesmo período de um pêndulo simples:

(b) Agora vamos fazer praticamente a mesma coisa para o outro caso. Temos a seguinte equação de torques:

A única diferença é a expressão para o momento de inércia, que para uma placa homogênea é:

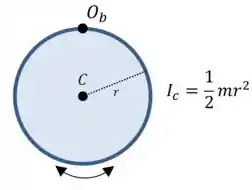
Então, pelo teorema dos eixos paralelos:

E substituindo na equação:

Agora vamos substituir e simplificar um pouco:

Fazendo , ficamos com:

Que dá a seguinte frequência angular:

E o seguinte período:

Que comparado ao período do pêndulo simples é:

(a) .

(b) .