Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.4 - Ex. 56
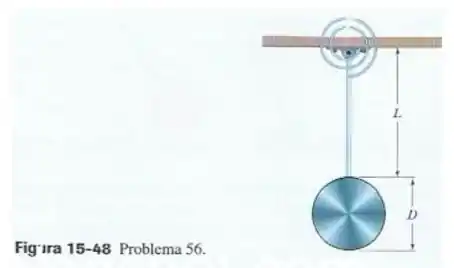
Na figura 15-48, um disco de com de diâmetro está preso a uma das extremidades de uma barra de comprimento e massa desprezível que está suspensa pela outra extremidade. (a) Com a mola de torção de massa desprezível desconectada, qual é o período de oscilação? (b) Com a mola de torção conectada, a barra fica em constante equilíbrio de na vertical. Qual é a constante de torção da mola se o período de oscilação diminuiu de ?
Passo 1
Primeiramente, vamos calcular o momento de inércia do sistema com relação ao ponto de articulação. Pra isso, a gente usa o teorema dos eixos paralelos para calcular o momento de inércia do disco com relação a o ponto de oscilação. Fica assim
Onde é o pino da dobradiça mostrado na figura (o ponto de suporte do pêndulo físico), cuja distância do centro do disco é . Logo, o período de oscilação sem a mola conectada é
Passo 2
Com a mola conectada agora, a equação do período muda um pouco de cara. Não é mais só a gravidade que exerce um torque sobre o pêndulo para que ele volta a posição de equilíbrio. A mola também ajuda a gravidade neste papel. Então, a nova equação para o cálculo do período é
O problema requer . Então . Isolando na equação, a gente tem que
Resposta
(a)
(b)