Enunciado
Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 15.1 - Ex. 26
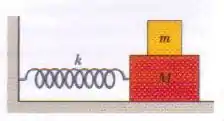
Na figura, dois blocos ( e ) e uma mola () estão dispostos em uma superfície horizontal sem atrito. O coeficiente de atrito estático entre os dois blocos é . Que amplitude do movimento harmônico simples do sistema blocos-mola faz com que o bloco menor fique na iminência de deslizar sobre o bloco maior?
Passo 1
Show de bolinhas galerinha bonita, tudo beleza?
Se liga só, nesse exercício aqui, temos dois blocos um em cima do outro, o primeiro tem massa enquanto que o segundo tem massa , o bloco de baixo está conectado a uma mola de constante elástica e estão dispostos em uma mesa horizontal sem atrito.
Sabendo que o coeficiente de atrito estático entre os dois blocos é , o enunciado quer que a gente encontre qual a amplitude do MHS do sistema blocos-mola faz com que o bloco menor fique na iminência de deslizar sobre o bloco maior.
Mas calma lá meu patrão, vamos com calma, primeiro vamos começar entendendo o que significa estar “na iminência de deslizar”. Bom, a gente sabe que, em geral, a força que impede o deslizamento é o atrito estático, dado como:
Onde é o coeficiente de atrito estático, e é a força normal, que nesse caso vai ser igual ao peso, já que o bloco laranja está bem apoiado no vermelho. Então:
Beleza. Agora ainda pensando no bloco laranja: com quem esse atrito vai competir? Bom, quando o bloco oscila junto com o resto do oscilador, ele tem uma aceleração, vamos chamar de (aceleração do oscilador). Então a força associada a isso é:
Passo 2
Iradoso, então quando ele está na iminência de deslizar, é porque a força de atrito já está resistindo o máximo possível, então:
E como queremos o caso limite, essa é a aceleração máxima do oscilador, uma fórmula que a gente já conhece bem é dada por:
Onde é amplitude do movimento, sendo assim, podemos igualar as equações de modo que:
E nosso objetivo é achar a amplitude que mantém essa situação aí. Então vamos isolar :
Já sabemos que e , falta achar o valor de . Bora lá!
Passo 3
A fórmula da frequência angular é:
Onde, nesse caso, é a constante elástica da mola, e é a massa total do sistema, segue que:
E substituindo isso na fórmula de cima, vamos obter que:
Portanto:
Pronto!
Resposta