Enunciado
Física - Randall D. Knight- Ed: 2º - Capítulo 14.Exercícios e Problemas - Ex. 17
Uma mola está pendurada no teto por um barbante. Quando um bloco é suspenso na extremidade livre do barbante, este estica a fim de atingir um novo valor de comprimento de equilíbrio. O bloco é, então, puxado levemente para baixo e é liberado. Com que freqüência ele oscilará?
Passo 1
A condição da mola e da massa no enunciado dado é a seguinte:
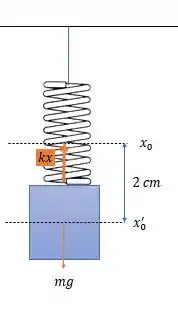
Onde é a nova posição de equilíbrio do sistema massa mola.
A frequência de oscilação bloco será calculado por:
Onde a constante elástica será dada por:
Então, substituindo os valores nós teremos:
Resposta
Exercícios de Livros Relacionados
68. Um bloco de massa M repousa sobre uma superfície sem atrito e está preso a uma mola horizontal cuja constante é k . A outra extremidade da mola está presa a uma parede (Figura 13.36 ) . Um segundo
74. Um fio de 1,80m de comprimento é suspenso verticalmente. Quando uma bola de aço de 60,0k g é suspensa na extremidade do fio, este se dilata 2,0m . Se a bola for puxada para baixo a uma distância a
67. Um prato uniforme, horizontal, de 1,50k g é preso a uma mola vertical ideal de constante igual a 185N / m , e uma esfera de metal de 275g está sobre o prato. A mola está sob o prato, podendo oscil
96. Duas molas, cada uma com um comprimento sem deformação igual a 0,200m , porém com constantes diferentes de equilíbrio, k 1 e k 2 , são ligadas as extremidades opostas de um bloco de massa m apoiad
99. Mola com massa. Em todos os problemas anteriores desse capítulo consideramos molas com massas desprezíveis. Porém, é claro que toda mola possui alguma massa. Para estudar o efeito da massa da mola