Os núcleos de um isótopo radioativo, que tem uma constante de decaimento , são produzidos num acelerador a uma taxa constante . O número de núcleos radiativos obedecem à equação .

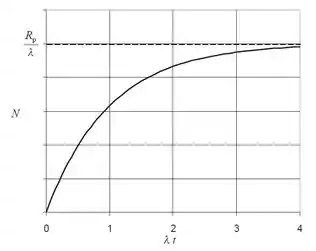
1. Se for zero em , faça um gráfico de contra para essa situação.
2. O isótopo de é produzido a uma taxa de por segundo, colocando cobre comum num feixe de fótons de alta energia. A reação é:

O isótopo de decai por decaimento e tem uma meia vida de . Depois de um tempo longo suficiente, tal que , quantos núcleos de ainda existem?

Oi pessoal, tudo bem?

Letra (a):

A equação diferencial é:

Agora vamos fazer a separação de variáveis, tudo que depende de de um lado e tudo que depende do tempo do outro:

E agora podemos integrar dos dois lados:

E isolando temos:

E usando um programa pra plotar um gráfico de versus obtemos: