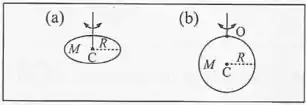
Uma placa circular homogêna de raio e massa é suspensa por um fio de módulo de torção de duas maneiras diferentes: (a) Pelo centro da placa, ficando ela num plano horizontal; (b) Por um ponto da periferia, com a placa vertical. Calcule os períodos e das pesquenas oscilações de torção, respectivamente nos casos (a) e (b).

(a) No primeiro caso, temos que calcular o momento de inércia em relação a um eixo perpendicular ao plano do disco, passando pelo seu centro:

Vamos considerar vários anéis de massa e largura , como o pintado de vermelho na figura:

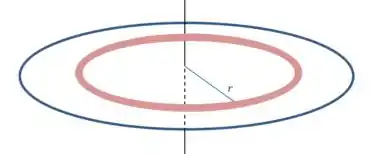
Se a densidade superficial do disco é:

Então a massa do disco é:

Substituindo isso na integral:

Agora é só integrar de até :

Então nesse caso a frequência angular é:

E o período é:

Agora temos que a fazer a conta em relação a um eixo paralelo ao plano do disco, também passando pelo seu centro:

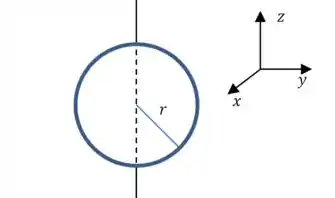
Aqui vamos tentar aproveitar o resultado do passo anterior. O raciocínio é um pouco complicado, então vamos por partes:

Tínhamos a seguinte expressão:

Que pode ser reescrita da seguinte forma:

Como estávamos no plano , o raio podia ser escrito em função de coordenadas cartesianas:

Nesse momento, e eram os eixos paralelos ao plano do disco. Por simetria, podemos afirmar que os dois são iguais, então:

Isso quer dizer que:

Integrando:

Então:

Beleza, achamos uma fórmula para o momento de inércia de um disco em relação a um eixo paralelo ao seu plano (passando pelo centro).

Bom, no caso da letra (b), estamos calculando justamente isso: o momento de inércia em relação a um eixo paralelo ao plano do disco.

Então temos:

E então a frequência angular é:

E o período é: