Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 13.Exercícios e Problemas - Ex. 20

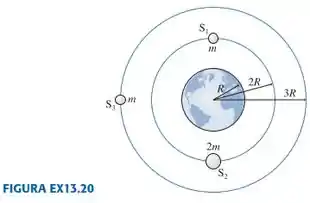
20 . || Três satélites orbitam um planeta de raio R , conforme ilustrado na F I G U R A   E X 13.20 . Os satélites S 1 e S 3 possuem massa m . O satélite S 2 tem massa igual a 2 m . O satélite S 1   completa uma órbita em 250   m i n u t o s , e a força exercida sobre ele é de 10.000   N .

a. Quais são os períodos de S 2 e de S 3 ?

b. Quais são as forças exercidas sobre S 2 e S 3 ?

c. Qual é a razão de energia cinética K 1 / K 3 para S 2 e S 3 ?

Passo 1

a. Quais são os períodos de S 2 e de S 3 ?

S 1 e S 2 estão na mesma orbita, logo T 1 = T 2

T 2 = 250   m i n u t o s

Sabemos que o período é:

T 2 = 4 π 2 R 3 G M P

Então adaptamos para cada um:

Para T 1

T 1 2 = 4 π 2 ( 2 R ) 3 G M P

T 1 = 8 ⋅ 4 π 2 ( R ) 3 G M P

Para T 3

T 3 2 = 4 π 2 ( 3 R ) 3 G M P

T 3 = 27 ⋅ 4 π 2 ( R ) 3 G M P

Podemos usar a razão entre T 3   e   T 1 e achar o próprio T 3 :

T 3 T 1 = 27 ⋅ 4 π 2 R 3 G M P 8 ⋅ 4 π 2 ( R ) 3 G M P

T 3 T 1 = 27 8

Sabemos que T 1 = 250 m i n u t o s  

T 3 = 27 8 ⋅ 250   m i n u t o s

T 3 = 459   m i n u t o s

Passo 2

b. Quais são as forças exercidas sobre S 2 e S 3 ?

Sabemos que :

F = G M P m R 2

Então:

Para F 1

F 1 = G M P m ( 2 R ) 2

F 1 = 1 4   ⋅ G M P m ( R ) 2

Para F 2

F 2 = G M P ( 2 m ) ( 2 R ) 2

F 2 = 2 4   ⋅ G M P m ( R ) 2

Assim juntando a última parte de cada desenvolvimento de F 1   e   F 2 :

4 F 1 = 2 F 2

4 ( 10000 N ) = 2 F 2

20000 N = F 2

Para F 3

F 3 = G M P m ( 3 R ) 2

F 3 = 1 9   ⋅ G M P m ( R ) 2

Assim juntando a última parte de cada desenvolvimento de F 1   e   F 3 :

4 F 1 = 9 F 3

4 ( 10000 N ) = 9 F 3

4444,44 N = F 3

Passo 3

c. Qual é a razão de energia cinética K 1 / K 3 para S 2 e S 3 ?

Usando a as fórmulas para Energia cinética:

E c = K = m v 2 2

Lembrando que velocidade orbital é:

v = G M R    

K 1 K 3 = M 1 v 1 2 2 M 3 v 2 2 2 = M 1 ⋅ G M 1 R 1   2   M 3 G M 3 R 3   2 = m G m 2 R   m G m 3 R = 3 2 = 1,5

Resposta

( a )

T 2 = 250 m i n u t o s

T 3 = 459   m i n u t o s

( b )

F 2 = 20000 N

F 3 = 4444,44 N

( c )

1,5

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

41. Um projétil é lançado da Terra na direção e no sentido do movimento terrestre em torno do Sol. Qual é o valor mínimo de velocidade que o projétil necessita ter com relação à Terra a fim de escapar
40. Um projétil é disparado para longe da Terra, em linha reta, a partir de uma base no lado oculto da Lua. Qual será a velocidade de escape do projétil do sistema Terra-Lua?
36. Um objeto de massa m é solto de uma altura h acima de um planeta de massa M e raio R . Obtenha uma expressão para a velocidade do objeto quando chegar ao solo.
39. Suponha que, na Terra, você consiga dar um pulo de 50c m de altura. Você conseguiria escapar de um asteróide de 4,0k m de diâmetro, com massa de 1,0 ⋅ 10 14k g ?
37. Dois meteoros estão se dirigindo à Terra. Ao cruzarem a órbita da Lua, os módulos de suas velocidades valem 2k m / s . O primeiro meteoro está se dirigindo diretamente para a Terra. Qual será a su