Movimento Harmônico Amortecido
Produzido por Leonardo de BemTeoria
O que é MHA?
A única coisa que muda em relação ao MHS é que agora tem atrito. Só isso!
MHA significa movimento harmônico amortecido.
Então o sistema não fica oscilando para sempre, ele vai parar com o tempo, porque a força de atrito vai tirando energia do sistema até ele parar. Nesse caso, a energia mecânica do sistema não se conserva!
Equação do MHA
Agora temos que acrescentar na Segunda Lei de Newton a força de atrito também.
Vamos ver o exemplo do sistema massa-mola.
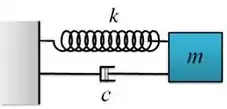
Observe que, nesse caso, além da mola com constante elástica , temos também um amortecedor, com constante de amortecimento .
Além do amortecedor, existem outros fatores que podem gerar atrito no sistema. Se o bloco estivesse mergulhado em um fluido viscoso, por exemplo, a força de atrito seria a força que o líquido exerce no bloco. Outro exemplo: se fosse uma mola vertical, um disco preso à massa faria com que a resistência do ar exercesse uma força de atrito também.
Mas em todos esses casos, a força de atrito é calculada da mesma maneira:
onde é a velocidade.
Assim como a força elástica é sempre contrária à posição, a força de amortecimento (atrito) também é.
Mas atrito não era ?
Era, mas nesse caso, estamos considerando atritos viscosos, que são sempre calculados daquela maneira. Esse atrito que aprendemos antes é o atrito seco.
Beleza, então vamos isolar o bloco e ver quais forças estão atuando nele:
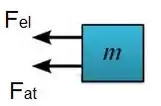
Então a força resultante é:
onde e
Observação: você também poderia dizer que , mas aí teria que dizer que e .
Substituindo na Segunda Lei de Newton:
Mas e
Então:
Logo:
Essa é a equação do MHA.
Observação: os coeficientes são sempre positivos! Se tiver algum negativo, verifique o sinal das forças, como fizemos antes no MHS.
Taí! Percebeu que fizemos os mesmos passos do MHS?
A única diferença é que apareceu um termo a mais nessa equação.
Se fizermos (atrito zero), teremos a equação do MHS.
E essa equação é uma EDO de 2ª ordem homogênea.
E como é que a gente resolve?
Vamos dar uma puxada lá no Cálculo! Quando temos uma EDO de 2ª ordem homogênea, resolvemos a equação auxiliar:
Dividindo todo mundo por
Agora, chamando e , vamos calcular o dessa equação:
E então temos três possibilidades:
Em cada caso, temos uma solução diferente, lembra?
Então vamos analisar cada uma dessas possibilidades agora.
Mas antes vamos dar nome aos bois:
Quando : amortecimento supercrítico;
Quando : amortecimento crítico;
Quando : amortecimento subcrítico;
É só você lembrar que “sub” significa “abaixo” (abaixo de zero) e “super” significa “acima” (acima de zero).
Beleza?
Então vamos lá!
Amortecimento supercrítico
Nesse caso:
Então a equação auxiliar tem duas raízes reais e distintas:
Chamando: e :
Lembrando que .
A solução é dada por:
As constantes e são dadas pelas condições iniciais de e .
O gráfico do amortecimento supercrítico tem essa cara:

Uma soma de exponenciais decrescentes.
Amortecimento crítico
Nesse caso:
Então a equação auxiliar tem duas raízes reais e iguais:
Porque o ((;).
A solução é dada por:
Ou, se preferir colocar em evidência:
As constantes e também são dadas pelas condições iniciais de e .
O gráfico do amortecimento crítico tem mais ou menos a mesma cara do amortecimento supercrítico (lembra que :

Como você pode perceber, o decai mais rapidamente nesse caso do que no caso supercrítico, mesmo o amortecimento sendo menor.
Amortecimento subcrítico
Nesse caso:
Então a equação auxiliar tem duas raízes imaginárias:
Chamando e :
Lembrando que .
E a solução é dada por:
Onde
As constantes e são sempre dadas pelas condições iniciais de e .
Dando uma sacudida nessas funções trigonométricas, a gente pode reescrever essa solução na forma
Agora, as constantes e são dadas pelas condições iniciais de e .
E o gráfico do amortecimento subcrítico tem uma cara assim:
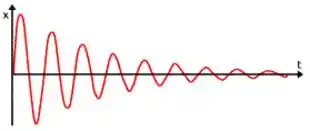
Nesse caso, o movimento é oscilatório, mas as amplitudes vão sendo cada vez menores, até parar.
Importante:não se preocupe em decorar essas soluções, caso você não lembre! Se for necessário, vai ter um formulário com elas. O mais importante é saber calcular e classificar o amortecimento em subcrítico, crítico ou supercrítico!
Obs: Lembre-se que o amortecimento que faz com o tenda a origem mais rapidamente é o crítico. Isso já caiu em algumas provas.
Considerações finais
Entendeu a ideia, então?
No fundo, estamos fazendo o mesmo que fizemos com MHS, só que considerando o atrito.
Uma observação importante: dissemos que a força de atrito é sempre da forma:
Depois era só substituir na Segunda Lei de Newton:
Mas se for o caso de ser a Segunda Lei de Newton de rotação:
O torque de atrito é dado por:
Entendeu? Seria o equivalente da rotação: o torque de atrito é proporcional à velocidade angular.
Será sempre assim a menos que o problema forneça outra expressão, beleza?
Outra observação: fizemos um exemplo de massa-mola, mas poderia ser um pêndulo ou qualquer outro sistema. Mas a ideia é a mesma. É só seguir o passo-a-passo!
Resumão
Ficou informação pra caramba, né? Vamos tentar dar uma revisada aqui nos pontos mais importantes.
- Equação do MHA:
- Tipos de amortecimento
Tem essa cara:
onde , e são positivos!
Força de amortecimento (atrito):
Torque de amortecimento (atrito):
onde é a constante de amortecimento.
Supercrítico:

Crítico:

Subcrítico:
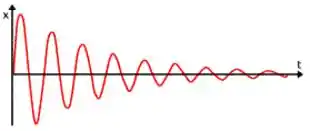
Amortecimento supercrítico
Amortecimento crítico
Amortecimento subcrítico
Considerações finais
Resumão
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P2-2013.2-M07
Um avião está voando em trajetória retilínea a uma altitude constante. De repente, ele é atingido por uma rajada de vento que faz força sobre sua parte frontal. O nariz do avião começa a oscilar por um dado período de tempo, assustando os passageiros, mas aos poucos a oscilação cessa e o avião volta a sua posição de equilíbrio. A situação apresentada representa:
- Um regime de oscilações não amortecidas, o avião oscila em movimento harmônico simples.
- Um regime de oscilações amortecidas, o avião oscila no regime subcrítico.
- Um regime de oscilações amortecidas, o avião oscila no regime supercrítico.
- Um regime de oscilações amortecidas, o avião oscila no regime crítico
- O avião entrou em ressonância com o vento.
Passo 1
O avião começou a oscilar aos poucos começou a parar o que isso te lembra?
Oscilações amortecidas, que é um Movimento Harmônico Amortecido, isso fica claro porque a oscilação para com o tempo.
A questão agora é qual tipo de oscilação amortecida o avião está tendo.
Lembra dos gráficos de MHA da teoria?
- Supercrítico
- Crítico
- Subcrítico


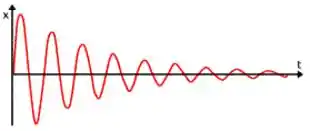
Os dois primeiros ele sobe uma vez e depois desce, o avião fica oscilando até parar, então temos um amortecimento subcrítico
Resposta
Letra B
Exercício Resolvido #2
UFRJ-P2-2014.2-Q5
Duas balanças são constituídas, cada uma, por uma mola e um prato, em que se deposita uma massa a ser medida. Observa-se que para a primeira balança, o prato não oscila, mas a balança demora um certo tempo para marcar o valor correto depois que a massa é posta no prato. Nota-se também que a segunda balança oscila várias vezes antes que o prato pare e esse valor possa ser lido. Assinale a alternativa INCORRETA:
- Na primeira balança observa-se um regime de amortecimento crítico ou supercrítico.
- Na segunda balança observa-se um regime de amortecimento subcrítico.
- Quanto mais amortecido o sistema, menos tempo a balança leva para marcar o valor correto.
- Se não houvesse nenhum tipo de amortecimento, a balança poderia oscilar por tempo indeterminado.
- O valor da massa altera a frequência natural de oscilação do sistema massa+prato+mola.
Passo 1
A gente tem que ver a balança como um sistema MHA.Vamos analisar uma por uma:
a) Verdadeira. Basta a gente perceber que não pode ser subcrítico se não tem oscilação.
b) Verdadeira. Palavra-chave: “oscila” Se oscila, só pode ser subcrítico.
c)Falsa! Se fosse assim, o regime supercrítico levaria o menor tempo pra parar. Sabemos que isso acontece pro crítico.
d)Verdade, pois seria apenas um sistema MHS. Ficaria oscilando indefinidamente.
e) Sim, pois a frequência angular é dada por:
Resposta
Letra c)
Exercício Resolvido #3
UFRJ-P2-2014.2-Q7
Um oscilador levemente amortecido tem seu parâmetro de amortecimento muito menor que sua frequência natural Neste caso a energia mecânica média armazenada no oscilador num dado instante de tempo é dada por . A vida média destas oscilações é definida como o intervalo de tempo no qual a energia média se reduz de um fator . O número de oscilações que a partícula realiza neste intervalo pode ser expresso por:
Passo 1
Vamos lá. Ali no enunciado tá sendo dito que o tempo de vida média, que vamos chamar de , é definido como o tempo que a energia média leva pra cair a um fator de do seu valor inicial.
Então vamos comparar com a expressão da energia pelo tempo pra descobrir quanto vale esse tempo de vida média:
Passo 2
Beleza, já achamos quanto vale esse tempo de vida média. Agora precisamos descobrir quantas oscilações ocorrem nesse tempo. Como pensamos nisso?
Bem, se você souber o período de oscilação, fica fácil. É só dividir o tempo pelo período.
Imagine um exemplo mais simples: Digamos que um sistema tenha um período de e seja posto pra oscilar durante .Quantas oscilações ele fez?
Quatro, pois : .
Passo 3
Então, vamos descobrir uma expressão pro período. Como é a frequência angular, temos que:
Agora vamos fazer aquilo que falamos: dividir o tempo de vida média por esse valor de período:
Resposta
a)
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume 2 : ondas, 8 ed. Rio de Janeiro : TLC, 2008, Cap 15, Problema 57.
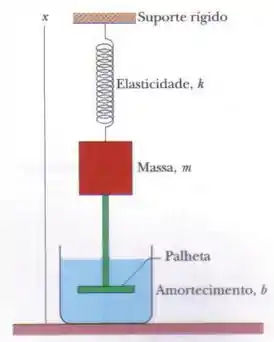
Na Fig. 15-15 o bloco possui uma massa de e a constante elástica é . A força de amortecimento é dada por , onde . O bloco é puxado para baixo e liberado. (a) Calcule o tempo necessário para que a amplitude das oscilações resultantes diminua para um terço do valor inicial. (b) Quantas oscilações o bloco realiza nesse intervalo de tempo?
Passo 1
Bom, sabemos que somente a força de amortecimento é responsável por diminuir a amplitude do movimento. Vamos fazer a equação característica:
E, calculando o :
Temos então um amortecimento subcrítico. O que podemos usar dessa informação? A equação geral! Isso mesmo!
Onde é a amplitude inicial do movimento e
Passo 2
- O termo antes do cosseno é a amplitude do movimento no momento , portanto, o que queremos é:
- Sabemos que:
Logo:
Passo 3
Com a velocidade angular em mãos podemos obter o período!
E o número de revoluções é dado por:
Como deve ser um número inteiro, podemos usar:
Resposta
Exercício Resolvido #5
USP-P1-2008-Q4
Um corpo preso na extremidade de uma mola e imerso em um fluido viscoso, executa um movimento harmônico amortecido no regime subcrítico, conforme a equação horária:
Sabendo-se que o corpo possui velocidade nula no instante , determine:
- A frequência natural de oscilação (frequência na ausência de força viscosa) do sistema massa-mola
- A fase inicial do movimento.
- O tempo necessário pra que a amplitude do movimento se reduza à metade do valor inicial.
Passo 1
Bem galera, a frequência angular de um sistema massa mola amortecido e a frequência angular natural se relacionam por:
Beleza. Analisando a equação do enunciado e comparando com o modelo:
A gente nota que:
E:
Então:
Passo 2
b)
A função da velocidade do MHA é calculada pela derivada da função
Usamos a regra do produto ali encima. Aplicando
Passo 3
c)
Pra calcular isso, a gente simplesmente precisa analisar só como a amplitude do movimento decai.
Isso é:
Como a amplitude vale precisamos descobrir qual o tempo que o sistema leva pra ficar com amplitude
Tirando logaritimos:
Resposta
a)
b)
c)
Exercício Resolvido #6
USP-P1-2009-Q4
Um corpo é pendurado de uma mola, colocado em vibração vertical e imerso em um béquer com óleo. Suponha que o corpo tenha massa , que a mola tenha constante de força e
- Quanto tempo leva pra amplitude cair pra metade de seu valor inicial?
- Quanto tempo leva pra energia mecânica cair pra metade de seu valor inicial?
- Demonstre que, de maneira geral, a taxa à qual a amplitude diminui em um oscilador harmônico amortecido é metade da taxa à qual a energia mecânica diminui.
Passo 1
a)
Bom, galera, essa questão trata de um MHA. Pra saber em que regime estamos temos que calcular aquele nosso amigo . Pelo enunciado temos
Assim
Como , estamos no regime sub-crítico!
Como sabemos a expressão pra oscilação de um MHA nesse regime é:
Onde
Beleza, mas nesse primeiro item, a gente só quer saber qual o tempo que é preciso pra que a amplitude caia à metade de seu valor inicial. Então vamos esquecer a parte do cosseno e escrever:
Usando :
Substituindo os valores do enunciado:
Passo 2
b)
Sendo a energia mecânica dada por:
A sua metade vale:
Mas a gente pode escrever esse nova energia mecânica em função de uma nova amplitude
Logo, fazendo parecido com o item anterior:
Substituindo os valores:
Passo 3
c)
Vamos calcular a derivada de energia mecânica dividida pela energia mecânica:
Beleza, mas pra que façamos uma comparação melhor, devemos normalizar isso dai. O que isso quer dizer? Que devemos calcular uma taxa relativa. Assim, vamos dividir os dois lados por
Viu? Assim conseguimos isolar o
Ou seja, como o lado direito possui a derivada da amplitude em relação, a gente conseguiu provar o que era preciso.
Resposta
a) s
b)
c) Demonstração