Oscilações Forçadas
Teoria
O que são oscilações forçadas?
Já vimos que pode existir uma força de amortecimento que “atrapalha” a oscilação. E se surgir, agora, uma força externa que também afete a oscilação, como a força peso?
Como assim? Veja a figura abaixo:
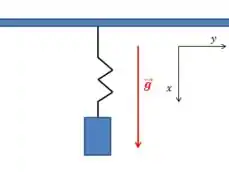
Chamamos isso de oscilação forçada.
Nesse caso, uma oscilação forçada com uma força que é constante no tempo.
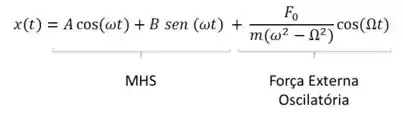
Matematicamente falando, antes estávamos lidando com EDOs Homogêneas. Agora, não mais. Então, a solução geral agora será dada pela soma de uma solução homogênea com uma solução particular:
Bora aprender a resolver isso.
Quando a força externa for constante
Vamos usar como exemplo de força constante a força peso, já comentada. Aliás, as chances de você encontrar uma questão envolvendo uma oscilação influenciada pela força peso são grandes.
Usando a segunda Lei de Newton aplicada ao exemplo lá de cima , vamos obter:
Ahh, mas lembra aí que podemos chamar a aceleração de . E dividindo tudo por m, temos:
Definimos :
Obs: Veja que o sentido do peso nesse caso é positivo pois eu adotei o sentido positivo de para baixo.
Beleza, chegamos a equação diferencial. Agora, como foi dito, a solução vai ser do tipo:
Para achar a solução homogênea, basta ignorarmos tudo que não é o x(t) ou suas derivadas. Então, é a solução da equação homogênea:
Que é uma equação simples de um MHS. Nós já vimos que essa solução é do tipo:
E agora, como achar a solução particular?
Bom, você deve lembrar de EDO que a gente “chuta” um valor pra solução particular que seja matematicamente parecido com a parte não-homogênea da equação e depois substitui na equação diferencial.
Nesse caso, como a parte não homogênea é uma constante (), então vamos chutar um valor constante também. Bem assim:
Substituindo na EDO:
Percebeu que a apareceu um zero ali porque a segunda derivada de uma constante é zero, né?
Lembrando que:
Então, no final:
Show? Ah, e se nesse caso tivesse um amortecimento?
Seria muito parecido, e solução particular seria a mesma. Por quê? Bom, porque as derivadas zerariam na EDO pelo mesmo motivo que antes:
O que mudaria seria a equação da parte homogênea, que depende do tipo de amortecimento, como vimos no capítulo de MHA.
E se a força for oscilatória?
Olhe a figura: Agora temos uma força externa que não é constante e que varia no tempo como uma força oscilatória:
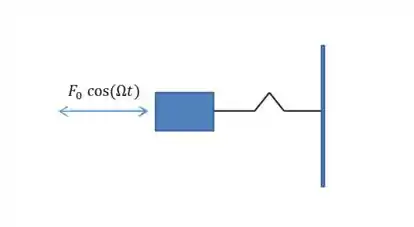
Por exemplo, quando você está empurrando um balanço para um amigo que está sentado.
Como vamos resolver isso? Simples, vamos partir da segunda Lei de Newton novamente.
Equacionando
Usamos a segunda lei de Newton para buscarmos uma solução, lembrando que nesse caso, não possuímos amortecimento:
Substituindo e dividindo tudo por m:
Fazendo .
Repare que é a frequência natural de oscilação da mola (um valor constante), mas é a frequência angular da oscilação externa (de valor variável). Não confunda as duas!!
Se liga, é um erro muito comum você chegar numa equação do tipo:
Mas isso está errado, pois no desenvolvimento da EDO a gente dividiu tudo pela massa. Preste atenção nisso!
Enfim, como vimos, a solução vai ser do tipo:
A solução homogênea é a solução de um MHS, mas a solução particular a gente vai precisar chutar, usando os métodos de EDOs.
Como a parte não homogênea é um cosseno, é de se esperar que a solução particular seja do tipo:
Vamos descobrir esse :
Assim:
Assim, na EDO:
Cortando os cossenos:
Então a solução particular vai ser:
A massa oscila com a frequência da força externa, sem diferença de fase. Se força empurra o balanço, ele vai pra frente, se você puxa, ele vai pra trás, como esperado.
Juntando tudo:
Ressonância
Repare na amplitude da solução particular que acabamos de achar.
A amplitude do movimento depende da frequência da oscilação externa ().
No caso do balanço, se você fica empurrando o balanço muito rápido (alta frequência) ou muito devagar (baixa frequência), a amplitude de oscilação vai ser baixa: seu amigo não se diverte.
Mas o que acontece quando a frequência externa fica igualzinha a frequência natural do sistema?
Quando , o denominador vai a zero!
A amplitude de oscilação vai ficando maior e maior até o infinito, como na figura abaixo. Chamamos esse fenômeno de RESSONÂNCIA!
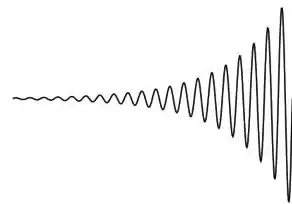
O máximo de amplitude só acontece quando o sistema entra em ressonância, isso é, quando ! Na ausência de amortecimento, a ressonância gera amplitudes infinitas!
Ou seja, se você quiser que seu amigo se divirta no balanço, você tem que empurrar com uma frequência próxima à frequência natural de oscilação do sistema para que ele tenha uma amplitude significativa. Mas cuidado, porque se não tiver atrito nenhum seu amigo vai sair voando para o infinito e além!
Agora é SUPER importante que você reforce todos os conceitos com os exercícios. Tanto os teóricos quanto os de conta, eles são essenciais para que você internalize os conhecimentos. BORA LÁ!!
E se a força for oscilatória?
Equacionando
Ressonância
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ-P2-2014.2-Discursiva 1
Considere um corpo de massa , preso a uma mola ( de constante elástica e comprimento relaxado cuja outra extremidade presa está presa ao teto. Considere que pode oscilar, sem resistência, na vertical sob a ação de um campo gravitacional O corpo é solto, inicialmente em repouso, da posição em que a mola encontra-se relaxada.
- DEDUZA a equação diferencial de movimento. Especifique CLARAMENTE o eixo e a origem de seu sistema de coordenadas.
- Mostre que a equação diferencial de movimento pode ser escrita como a equação do oscilador harmônico simples em torno de uma nova posição de equilíbrio e determine esta posição.
- Escreva a solução completa que descreve o movimento, em função dos dados do problema.
Passo 1
Vamos definir nosso eixo de coordenadas apontando pra baixo, na direção do vetor peso:
A nossa origem ficará no teto. A força elástica será dada por:
Onde é o deslocamento e o vetor unitário que aponta na direção de Como o comprimento natural é , temos que:
Show! Então a força elástica vai ser:
E temos também a força peso, né? É de se esperar que ela seja positiva, pois aponta na direção de crescimento do
Vamos calcular agora a força resultante usando a segunda lei de Newton:
A aceleração, no caso, é a segunda derivada da posição em relação ao tempo:
Então:
(:
Passo 2
b)
Bom, primeiro, qual é posição de equilíbrio galera?
Vamos definir como:
Ou seja, o comprimento que gera uma força elástica que equilibra o peso. Agora, vamos definir novas coordenadas
Então, reescrevendo a equação diferencial que a gente encontrou (Trocando só por ):
Substituindo o valor de
Primero: A derivada de elimina constante
Logo:
Passo 3
c):
Vamos calcular a solução para . Como o sistema é forçado, a solução será composta por uma solução homogênea e uma particular. A solução homogênea será do tipo:
E a solução particular?
Bom, a solução particular vai ser do tipo:
Onde é uma constante. Isso seve ao fato de que a força externa é constante. Então, substituindo na expressão:
Logo, a solução geral vai ser do tipo:
As condições iniciais são:
Lembrando-se que a mola parte do repouso, por isso .Então:
Passo 4
Calculando a derivada da solução a aplicando em
Logo:
Com
Vamos escolher Logo:
Então, voltando a expressão que achamos pra :
Então, finalmente, a solução será:
Resposta
a):
b):
c):
Exercício Resolvido #2
UNICAMP-Questão 1 - P2.2012 (Noturno)
No sistema bloco-massa da figura, o bloco possui uma massa de e a mola possui massa desprezível. O sistema está sobre uma superfície sem atrito que faz um ângulo de com a horizontal.
- Sabendo que quando o sistema está em equilíbrio estático a mola sofre uma elongação de , calcule a constante da mola.
- Em seguida, a mola é puxada mais e depois solta em . Encontre a frequência angular e o período .
- Determine a equação de movimento, a velocidade e a aceleração.
Se necessário use e .
Passo 1
a)
Quando o bloco está em equilíbrio, a força da mola equilibra o peso na direção do plano inclinado:
Então:
Passo 2
b)
Ai vem um macete: A frequência angular só depende da constante da mola e da massa do bloco. Logo:
E o período:
Passo 3
c)
Vamos montar a EDO responsável pelo movimento. As forças que agem sobre o bloco são a força peso, no caso a sua componente na direção do plano, e a força elástica. Logo:
O sinal do peso é negativo devido ao eixo que arbitrado na figura. Logo:
Bo resolver isso como a gente aprendeu a resolver uma EDO. Vamos resolver a equação homogênea primeiro:
E equação relacionada será:
Como é complexo, a solução da homogênea será:
E a solução particular será:
Onde é uma constante. Logo:
Logo:
Agora vamos parra as condições de contorno. Vamos considerar como a nossa origem o ponto de equilíbrio do sistema. Então, o deslocamento inicial será Então, para :
:
E como o bloco parte do repouso, Derivando a expressão acima e substituindo os valores:
Logo a solução é:
Então a velocidade será dada por
E a aceleração será dada por
Resposta
a)
b)
c)
Exercício Resolvido #3
UNICAMP-Questão 1 - P2.2012
Um bloco de massa desliza sem atrito sobre um plano inclinado que faz um ângulo com a horizontal e tem uma mola fixa no final da rampa. O bloco é solto de uma posição inicial tal que a distância entre a ponta livre da mola e a face do bloco é . Quando o bloco bate na mola, um dispositivo é acionado conectando o bloco na mola. O bloco comprime a mola até um valor máximo igual a , quando a velocidade instantânea do bloco torna-se zero. Considere um eixo ao longo do plano inclinado no sentido descendente e com sua origem na posição da ponta livre da mola quando ela não está deformada. Determine, em função dos parâmetros fornecidos e da aceleração da gravidade no local:
- A frequência angular do movimento harmônico simples que o bloco executa após conectar-se à mola.
- A posição na qual a velocidade do bloco é máxima.
- A posição mais alta que o bloco alcança após conectar-se à mola.
Passo 1
Vamos, primeiramente, escrever a equação diferencial associada ao bloco:
Bom, quais são as forças que atuam sobre o bloco?
As forças que atuam sobre o bloco são a força peso e a força elástica.
Então, pela segunda lei de Newton:
No entanto, como estamos lidando com um plano inclinado, a força peso terá apenas uma componente (lembra disso em mecânica?(: ):
E a força elástica é:
Logo, agora se importando apenas com os módulos:
Sendo :
Passo 2
a)
Aqui a questão pede a frequência angular. A gente sabe que a frequência angular aparece, elevado ao quadrado, na nossa EDO como o termo que acompanha o :
Logo:
Só que a gente não sabe quem é ! Não foi dado no problema. HUUM, vamos ter que pensar um pouco aqui.
Bem, o enunciado diz que o bloco estava afastado por uma distância da origem estabelecida na figura, e que, depois que ele toca na mola, o mesmo ainda se afasta na direção negativa de .
Por isso a gente pode montar a figura:
O valor do cateto do triangulo é esse graças ao valor de . Logo, sabemos que o o bloco saiu de uma para uma altura zero. Então vamos aplicar a conservação da energia:
No início havia apenas energia potencial gravitacional, e no fim passou a ter apenas energia potencial elástica, ou seja:
Logo:
Passo 3
b)
Bem, após a conexão com a mola, o bloco vai passar a oscilar em torno do ponto determinado pela figura da questão com uma amplitude .
Quando o bloco atinge os seus extremos de oscilação, ou , a sua velocidade é zero, pelo que sabemos do estudo dos MHS, logo, nesses pontos, a energia é toda potencial elástica.
E quando ele passa pelo ponto , como não há deslocamento , a sua velocidade é máxima, pois nesse caso a energia é toda cinética.
Logo, o ponto para o qual a velocidade é máxima é o ponto
Passo 4
c)
Aqui a gente pode fazer de uma forma muito simples, usando de novo a conservação da energia. Quando o bloco está na posição mais baixa, com a altura vertical , a sua energia é toda elástica. Como a energia se conserva, quando ele estiver na altura máxima, a mesma valerá:
Onde vai ser o valor da elongação. Logo, a energia no segundo instante será a soma da energia potencial gravitacional mais a energia potencial da mola. Por conservação da energia mecânica:
Resolvendo a equação em e lembrando do valor de :
Logo, a altura máxima é:
Resposta
a)
b)
c)