Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Energia Cinética Relativística

Ver Todos os Exercícios

Teoria

Até então, sempre que trabalhávamos com energia cinética, usávamos a seguinte expressão:

K = 1 2 m v 2

Essa expressão é uma boa aproximação para os casos em que v ≪ c .

No entanto, partindo da expressão da Energia Total Relativística, podemos dizer que a expressão para energia cinética K é dada por:

K = E - E 0

K = γ m c 2 - m c 2

K = m c 2 γ - 1

E n e r g i a   c i n é t i c a   r e l a t i v í s t i c a

Onde γ é o fator de Lorentz, dado por:

γ = 1 1 - v 2 c 2

Graficamente, é isso o que acontece:

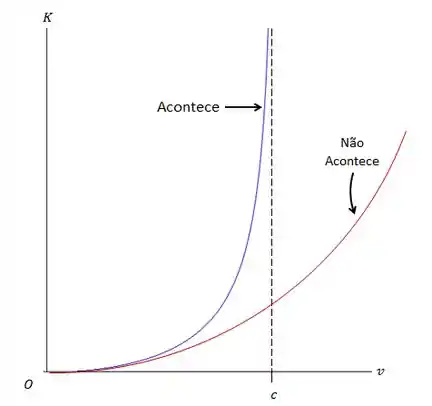
A linha vermelha representa a expressão da energia cinética não relativística (que sempre usávamos até então), e a linha azul representa a expressão da energia cinética relativística (que, de fato, acontece).

Equivalência entre Massa e Energia

Lembra lá!

O primeiro postulado da relatividade diz que:

“As leis da física são as mesmas em todos os referenciais inerciais. Não existe um referencial absoluto.”.

Portanto, isso deve ser válido também para a lei de conservação de energia. Assim, não importa o que aconteça, a seguinte afirmação deve continuar sendo válida:

“A energia total de um sistema isolado não pode mudar.”

Conservação de Energia

Como a energia se conserva, se a energia de repouso total de um sistema isolado de duas partículas diminui, algum outro tipo de energia deve aumentar, para que a energia total do sistema permaneça constante.

Nas relações químicas e nucleares, a variação da energia de repouso do sistema devido à reação é determinada a partir do valor de Q , através da seguinte equação:

E 0 i = E 0 f + Q

Onde E 0 i e E 0 f são as energias de repouso inicial e final do sistema, respectivamente.

Usando a relação E 0 = m c 2 , podemos reescrever o valor de Q da seguinte forma:

Q = - Δ M c 2

Onde:

Δ M = M f - M i

Sendo M f e M i as massas final e inicial do sistema, respectivamente.

Assim, a variação de energia é descrita pela variação de massa. É isso, vamos praticar?

Equivalência entre Massa e Energia

Conservação de Energia

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 180-43.

A massa de um elétron é 9,109   381   88 × 10 - 31 k g . Determine, com seis algarismos significativos, a o valor de γ e b o valor de β para um elétron com energia cinética K = 100   M e V .

Passo 1

a Determine, com seis algarismos significativos, o valor de γ .

Por definição, a energia cinética relativística é dada por:

K = m c 2 γ - 1

Isolando γ , teremos:

γ = K m c 2 + 1

Agora é partir pras contas.

Passo 2

Onde:

K = 100   M e V = 100 × 10 6 × 1,6 × 10 - 19 = 1,6 × 10 - 11   J

m = 9,109   381   88 × 10 - 31 k g

c = 3 × 10 8   m / s

Logo:

γ = 1,6 × 10 - 11 9,109   381   88 × 10 - 31 × 3 × 10 8 2 + 1

γ ≅ 196,471

Passo 3

b Determine, com seis algarismos significativos, o valor de β .

Sabemos que γ e β estão relacionados por:

γ = 1 1 - β 2

Logo, β será dado por:

γ 2 = 1 1 - β 2

β 2 = 1 - 1 γ 2

β = 1 - 1 γ 2

Substituindo o valor que achamos no item anterior, teremos:

β = 1 - 1 196,471 2

β = 0,999987

Resposta

a

γ ≅ 196,471

b

β = 0,999987

Exercício Resolvido #2

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 180-40.

Determine a menor energia necessária para transformar um núcleo C 12 (cuja massa é 11,996   71   u ) em três núcleos de H e 4 (que possuem uma massa de 4,001   51   u cada um).

Passo 1

A menor energia necessária para realizar essa transformação é a diferença de energia entre os dois estados é dada por:

Q = - Δ M c 2

Q = - M f - M i c 2

Substituindo os valores das massas, teremos:

Q = - 3 × 4,001   51   u - 11,996   71   u c 2

Q = - 0,00782 u c 2

Obs.: Para se determinar a massa de um átomo ou molécula em gramas g , divide-se o valor da massa molar pelo número de Avogrado 6,022 × 10 23   m o l - 1 .

Onde:

1 u = 10 - 3 6,022 × 10 23 k g

c = 3 × 10 8   m / s

Logo:

Q = - 0,00782 × 10 - 3 6,022 × 10 23 × 3 × 10 8 2

Q = - 1,1687 × 10 - 12 J = - 7,29 M e V

Resposta

Q = - 1,1687 × 10 - 12 J = - 7,29 M e V

Exercício Resolvido #3

PUCRIO-P3-2013.2-1c

c ) A energia total de um próton é 2,0   G e V . Calcule a energia cinética ( K e ) em G e V e a velocidade ( u ) desse próton em função de c . A energia de repouso do próton é 0,938   G e V .

Passo 1

Vamos primeiro calcular a energia cinética desse próton. Para isso, vamos lembrar da definição de energia total:

E = m . c 2 + K

Para o próton, temos:

E p = m p . c 2 + K p

Como temos o valor da energia total, e sabemos que a energia de repouso é dada por:

m p . c 2 = 0,938   G e V

Podemos calcular a energia cinética:

2,0 = 0,938 + K p

Ahh...como está tudo em G e V , não precisamos nos preocupar em igualar as unidades. Mas fique sempre atento para as unidades!

K p = 1,062   G e V

Passo 2

Agora, vamos calcular a velocidade desse próton. Para isso, vamos lembrar a definição da energia cinética que leva em conta os efeitos relativísticos:

K = m . c 2 . γ - 1

Onde γ = 1 / 1 - v c 2 é o chamado fator de Lorentz.

Vamos primeiro determinar o valor do fator de Lorentz par depois determinar a velocidade. Então, voltando à energia cinética, temos:

K p = m p . c 2 ( γ - 1 )

Substituindo os valores, temos:

1,062 = 0,938 ( γ - 1 )

γ = 2,13

Passo 3

Agora vamos determinar a velocidade em função de c utilizando a definição do fator de Lorentz:

γ = 1 1 - v c 2

Substituindo, temos:

2,13 = 1 1 - v c 2

1 - v c 2 = 1 2,13 2

- v c 2 = 0,22 - 1

v c = 0,78

v c = 0,883

v = 0,883 c

u = 0,883 c

Resposta

K p = 1,062   G e V

u = 0,883 c

Exercício Resolvido #4

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 180-42.

As massas das partículas envolvidas na reação p + F 19 → α + O 16 são as seguintes:

m p = 1,007   825   u

m F = 18,998   405   u

m α = 4,002   603   u

m O = 15,994   915   u

Calcule o Q da reação.

Passo 1

Por definição, o Q é dado por:

Q = - Δ M c 2

Q = - M f - M i c 2

Vamos começar substituindo os valores das massas:

Q = - 4,002   603   u + 15,994   915   u - 1,007   825   u + 18,998   405   u c 2

Q = 0,008712   u c 2

Obs.: Para se determinar a massa de um átomo ou molécula em gramas g , divide-se o valor da massa molar pelo número de Avogrado 6,022 × 10 23   m o l - 1 .

Onde:

1 u = 10 - 3 6,022 × 10 23 k g

c = 3 × 10 8   m / s

Logo:

Q = 0,008712 × 10 - 3 6,022 × 10 23 × 3 × 10 8 2

Q = 1,302 × 10 - 12 J = 8,12   M e V

Resposta

Q = 1,302 × 10 - 12 J = 8,12   M e V

Exercício Resolvido #5

Young e Freedman, Física IV Ótica e Física Moderna, 12ª ed, São Paulo: Addison Wesley, 2009, cap 37, pp 174 – 37.41.

Calcule a energia cinética de um próton (massa igual a 1,67 × 10 - 27   k g ) usando a expressão relativística e também a expressão não-relativística e calcule a razão entre os dois resultados (relativística dividida pela não-relativística) para velocidades de

a)   8,0 × 10 7   m / s

b)   2,85 × 10 8   m / s

Passo 1

A expressão relativística é dada por:

K r = E - m c 2

K r = γ m c 2 - m c 2 = γ - 1 m c 2

A expressão não-relativística é dada por:

K n r = 1 2 m v 2

Onde m = 1,67 × 10 - 27   k g .

Passo 2

Letra (a): v = 8,0 × 10 7   m / s

Energia cinética relativística:

γ = 1 1 - v 2 / c 2

Onde c = 3 × 10 8   m / s .

γ = 1 1 - 8,0 × 10 7 3 × 10 8 2   = 1,0375

Assim:

K r = γ - 1 m c 2

Onde:

γ = 1,0375 ;

m = 1,67 × 10 - 27   k g ;

c = 3 × 10 8   m / s ;

Logo:

K r = 1,0375 - 1 × 1,67 × 10 - 27 × 3 × 10 8 2

K r = 5,65 × 10 - 12 J

Passo 3

Energia cinética não-relativística:

K n r = 1 2 m v 2

Onde:

m = 1,67 × 10 - 27   k g ;

v = 8,0 × 10 7   m / s ;

Logo:

K n r = 0,5 × 1,67 × 10 - 27 × 8,0 × 10 7 2

K n r = 5,34 × 10 - 12 J

Passo 4

K r K n r = 5,65 × 10 - 12 5,34 × 10 - 12 = 1,06

Passo 5

Letra (b): v = 2,85 × 10 8   m / s

Energia cinética relativística:

γ = 1 1 - v 2 / c 2

Onde c = 3 × 10 8   m / s .

γ = 1 1 - 2,85 × 10 8 3 × 10 8 2   = 3,2025

Assim:

K r = γ - 1 m c 2

Onde:

γ = 3,2025 ;

m = 1,67 × 10 - 27   k g ;

c = 3 × 10 8   m / s ;

Logo:

K r = 3,2025 - 1 × 1,67 × 10 - 27 × 3 × 10 8 2

K r = 3,31 × 10 - 10 J

Passo 6

Energia cinética não-relativística:

K n r = 1 2 m v 2

Onde:

m = 1,67 × 10 - 27   k g ;

v = 2,85 × 10 8   m / s ;

Logo:

K n r = 0,5 × 1,67 × 10 - 27 × 2,85 × 10 8 2

K n r = 6,78 × 10 - 11 J

Passo 7

K r K n r = 3,31 × 10 - 10 6,78 × 10 - 11 = 4,88

Resposta

Letra (a):

Não-relativística: 5,34 × 10 - 12 J

Relativística: 5,65 × 10 - 12 J

1,06

Letra (b):

Não-relativística: 6,78 × 10 - 11 J

Relativística: 3,31 × 10 - 10 J

4,88

Exercício Resolvido #6

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 180.

a A energia liberada pela explosão de 1,0   m o l de T N T é 3,40   M J . A massa molar do T N T é 0,27   k g / m o l . Que peso de T N T seria necessário para liberar uma energia de 1,80 × 10 14 J ?

b Esse peso poderia ser carregado em uma mochila ou seria necessário usar um caminhão?

c Suponha que na explosão de uma bomba de fissão 0,080 % de massa físsil seja convertida em energia. Que peso de material físsil seria necessário para liberar uma energia de 1,80 × 10 14 J ?

d Esse peso poderia ser carregado em uma mochila ou seria necessário usar um caminhão?

Passo 1

Primeiro, vamos resolver a letra a .

Sabemos que ao explodir, cada mol de T N T libera uma energia de 3,40   M J = 3,40 ⋅ 10 6   J .

Contudo, usando a massa molar da T N T , notamos que 1 mol de T N T equivale a 0,27   k g . Agora, podemos fazer a regra de três.

Se 0,27   k g de T N T liberam 3,40 ⋅ 10 6   J de energia ao explodir, então a energia liberada por 1 k g vai ser:

3,40 ⋅ 10 6 0,27 ≅ 12,59 ⋅ 10 6   J / k g  

Para termos uma energia de 1,8 ⋅ 10 4   J , precisaremos de uma massa de T N T de

m = 1,8 ⋅ 10 14 12,59 ⋅ 10 6 ≅ 0,1429 ⋅ 10 8   k g = 14290 ⋅ 10 3   k g = 14290   t o n

Passo 2

Quanto à letra b , eu não sei na sua mochila, mas na minha definitivamente não cabem 14 mil toneladas de T N T !!! Então eu usaria um caminhão.

Passo 3

Para a bomba físsil, usando a equação de Einstein, a energia liberada seria de:

Q = - Δ E = E i n i c i a l - E f i n a l = M i c 2 - M f c 2 = M i - M f c 2

Como 0,080 % da massa foi convertida em energia, temos que a variação da massa foi de 0,080 % da massa inicial. Logo:

Q = 0,080 100 ⋅ M i c 2

Para liberar uma energia de 1,80 ⋅ 10 14   J , sendo a velocidade da luz no vácuo aproximadamente igual a c ≅ 3 ⋅ 10 8   m / s , a massa de material físsil necessária seria:

M i = 100 0,080 ⋅ Q c 2 = 100 ⋅ 1,80 ⋅ 10 14 0,080 ⋅ 3 2 ⋅ 10 16 = 2,5   k g

Passo 4

Agora, respondendo a letra d , isso aí é fácil de carregar na mochila. Só pra você ter noção, o livro de cálculo do Stewart e o livro de física do Halliday juntos pesam 2,4   k g só!

(Embora eu não carregaria material nuclear na minha mochila, mas cada um faz o que quiser né.)

Resposta

Letra a

m = 14290   t o n

Letra b

Teria que carregar em um caminhão.

Letra c

M i = 2,5   k g

Letra d

É leve o suficiente pra ser carregado na mochila (embora não recomendável).

Exercícios de Livros Relacionados

53. Dizemos que uma partícula é extremamente relativística quando sua energia cinética é muito maior do que sua energia de repouso. a ) Qual é a velocidade de uma partícula (expressa como uma fração d
58. Um fóton com energia E é emitido por um átomo de massa m que recua em sentido contrário. a ) Supondo que o movimento do átomo possa ser tratado de modo não-relativístico, calcule a velocidade de r
56. Uma bomba atômica contendo 8,0k g de plutônio explode. A soma das massas de repouso dos produtos da reação é menor uma parte em 10 4 do que as massas de repouso antes da reação. a ) Qual é a energ
55.O Grande Colisor de Hádrons (LHC). Físicos e engenheiros do mundo todo se juntaram para construir o maior acelerador do mundo, o Grande Colisor de Hádrons (Large Hadron Collider - LHC) nos laborató
60. Suponha que a velocidade dos prótons do Problema 37.59 seja tal que cada próton apresenta uma velocidade que é a metade da velocidade da luz em relação ao outro próton. a ) Qual é a velocidade des