PUCRIO – Física 3 2020.2 – G4 – Questão 3
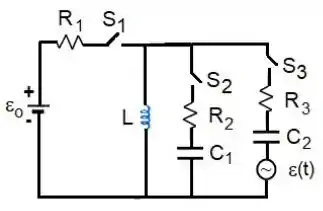
No circuito da Figura, os elementos conhecidos têm os seguintes valores: , , , e . Inicialmente, todas as chaves estão abertas, o capacitor tem uma carga desconhecida, o capacitor está descarregado e não existe corrente no indutor . Na FASE 1, apenas a chave é fechada. Imediatamente após o fechamento desta chave, mede-se a corrente A no circuito relevante, sendo o tempo expresso em segundos. Com base nestas informações:
a) Determine os valores de e , indicando o sentido da corrente no circuito (horário ou anti-horário) muito tempo após o fechamento da chave .
b) Calcule a energia armazenada no indutor L muito tempo após o fechamento da chave .
Passo 1
Fala galera, tudo bem? Vou ajudar você aqui!
Letra (a):
Da expressão para a corrente temos:
E sabemos que o indutor se comporta como um fio condutor normal, e daí a malha fica apenas com o resistor :
E do argumento da exponencial temos o seguinte:
Daí temos que a constante é:
E o sentido da corrente? É para baixo no indutor, ou seja, em sentido horário, conforme a bateria.
Passo 2
Letra (b):
A energia armazenada no indutor é proporcional à corrente final. A corrente para é , daí usando o valor da indutância que encontramos no passo anterior, podemos achar o valor da energia armazenada:
Beleza?
Espero ter te ajudado!