Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Fontes de CA e Reatância

Ver Teoria
Exercício 1234567

Enunciado

Em um circuito formado por um indutor e uma fonte C A a reatância indutiva vale X L = 100 Ω . A voltagem de pico da fonte vale 10   V . Sabendo que no instante t = π   10 - 3   s a corrente instantânea vale 10 - 2   A , determine:

a ) A frequência ω

b ) A indutância do indutor.

c ) Faça o gráfico dos fasores da corrente e das voltagens no indutor e na fonte.

d ) Esboce o gráfico das funções v L ,   ε e i (os gráficos devem estar superpostos no mesmo sistema de eixos cartesianos).

Passo 1

a )

Para determinar a frequência, podemos usar a equação da corrente em um circuito CA com carga indutiva:

i L = V L X L . sen ⁡ ω d . t - π 2

Substituindo os valores dados no enunciado, temos:

10 - 2 = 10 100 . sen ⁡ ω d . π . 10 - 3 - π 2

0.1 = sen ⁡ ω d . π . 10 - 3 - π 2

Agora a gente tem que tirar o arcoseno dos dois lados da equação

0,1 = ω d . 10 - 3 - 1 2 . π

ω d . 10 - 3 - 1 2 ≈ 0,032

ω d = 5,32 × 10 2   r a d / s

Passo 2

b )

Para determinar a Indutância, podemos usar a fórmula da definição da reatância indutiva:

X L = ω d . L

Substituindo os valores, temos:

100 = 5,32 × 10 2 . L

L = 188   m H

Passo 3

c )

Para determinar o diagrama de fasores, precisamos lembrar que a corrente está atrasada π 2 em relação à tensão. Por ser apenas um circuito CA com um indutor, a tensão na fonte será a mesma tensão no indutor. Logo, o diagrama de fases para um tempo arbitrário será:

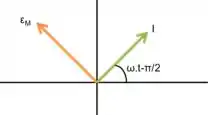
Passo 4

d )

Para esboçar os gráficos de v L , ε e i , vamos primeiro relembrar essas equações:

i L t = 0,1 . sen ⁡ 5,32 × 10 2 . t - π 2

v L t = ε t = 10 . sen ⁡ 5,32 × 10 2 . t

Logo, os gráficos ficaram:

Resposta

a ) ω d = 5,32 × 10 2   r a d / s

b ) L = 188   m H

Exercícios de Livros Relacionados

Um circuito RLC série possui uma frequência de ressonância de 6,00k H z . Quando o circuito é excitado com uma frequência de 8,00k H z , possui uma impedância de 1,00k Ω e uma constante de fase de 45
Na Fig. 31-32, um gerador de frequência ajustável é ligado a um circuito formado pela resistência R = 100Ω , as indutâncias L 1 = 1,70m H e L 2 = 2,30m H e as capacitâncias C 1 = 4,00μ F , C 2 = 2,50μ
(a) Em um circuito R L C , a amplitude da tensão entre os terminais do indutor pode ser maior que a força eletromotriz do gerador? (b) Considere um circuito R L C com ε = 10V , R = 10Ω , L = 1,0H e C
Um circuito R L C como o da Fig. 31-7 tem R = 5,00Ω , C = 20,0μ F , L = 1,00H e ε = 30,0V . (a) Para que frequência angular ω d a amplitude da corrente é máxima, como nas curvas de ressonância da Fig.
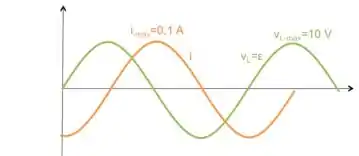
Uma fonte alternada de frequência variável f d é ligada em série com um resistor de 8 0,0Ω e um indutor de 4 0,0m H . A amplitude da força eletromotriz é 6 , 0 0V . (a) Desenhe um diagrama fasorial pa