Calcule a entalpia das reações a seguir, usando os valores de energias de ligação listadas abaixo:
Passo 1
O primeiro passo é ver se as reações ali estão balanceadas.
No lado dos reagentes da primeira reação a gente tem 8H e 3C. Nos produtos da mesma reação temos 3C e 8H. Tá balanceada.
Na segunda reação, no lado dos reagentes temos 4C (2 x 2), 12H (2 x 6) e 14O (7 x 2). Nos produtos temos 4C, 14O (4 x 2 + 6) e 12H (6 x 2). Tá balanceada também.
Beleza, foi só por precaução.
Passo 2
Pra saber quantas ligações vamos ter que quebrar e quantas serão formadas a gente precisa conhecer a fórmula estrutural daquelas moléculas.
Pra primeira reação:
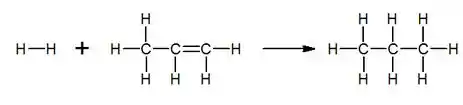
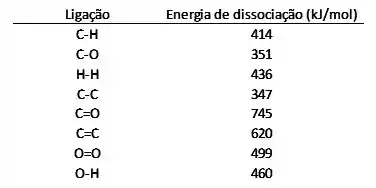
E pra segunda:

Passo 3
Pra primeira reação:
Você até pode quebrar todas as ligações ali nos reagentes e depois formar todas as ligações dos produtos.
Mas é bem mais fácil mexer só no que tá mexido né? Tipo assim, só contar a energia das ligações que realmente estão sendo quebradas e das que realmente estão sendo formadas.
Olhando pras estruturas, a gente pode dizer que a ligação H – H do H2 e a dupla ligação C = C do C3H6 foram quebradas.
Olhando a tabela das energias de dissociação, a energia que a gente precisa dar para o sistema a fim de quebrar essas ligações é calculada por:
Não se esquece que ao usar a energia 620 kJ, a gente quebra as duas ligações da dupla! É como se agora nossas moléculas estivessem assim:
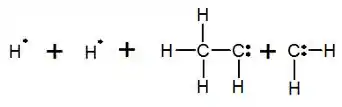
E pra formar os produtos, a gente precisa formas duas ligações C – H e uma C – C.
Como ao formar ligações o sistema libera energia e energia liberada fica com sinal negativo, a variação de entalpia da reação é dada por:
Ou seja, a cada mol de C3H8 formado a partir daquela reação, libera-se 119 kJ.
Passo 4
Fazendo a mesma coisa pra segunda reação, com um pouco mais de cuidado porque todas as moléculas envolvidas tem um índice na frente que indica o número de mols da molécula envolvido na reação.

Aqui não tem jeito, vamos ter que quebrar tudo e montar tudo de novo.
No C2H6 a gente tem 6 ligações C – H e 1 ligação C – C.
Mas a gente tem dois mols dessa molécula, então:
No O2 temos uma ligação O = O:
Mas temos 7 mols de O2, então:
Pros produtos, agora.
Pra cada mol de CO2, temos que formar 2 ligações do tipo C = O:
Mas são 4 mols de CO2, então:
E cada mol de H2O tem 2 ligações H – O:
Pra 6 mols de H2O:
Passo 5
Como energia pra quebrar ligação é positiva e energia de ligação formada é negativa, a variação de entalpia da reação é dada por:
E a segunda reação libera 2.325 kJ!
Resposta