Uma partícula alfa se move com uma velocidade de módulo em uma região onde existe um campo magnético de módulo . (Uma partícula alfa possui uma carga e uma massa ). O ângulo entre e é .
Dados:
Determine:
- O módulo da força que o campo magnético exerce sobre a partícula.
- A aceleração da partícula causada por
- A velocidade da partícula aumenta, diminui ou permanece constante?
Passo 1
Não se preocupe, você já viu isso tudo e vamos fazer essa questão para você ficar ainda mais craque nesse assunto.
No enunciado já pede de cara o módulo da força magnética e já te dá os seguintes elementos:
Módulo da velocidade:
Módulo do campo magnético:
Carga:
Nós sabemos que a fórmula para encontrar a força magnética é:
E você sabe também que o produto vetorial pode ser substituído pela expressão que depende do ângulo entre eles. Dessa forma:
Logo, temos:
Passo 2
Sendo que como o ângulo entre a velocidade e o campo magnético é , podemos substituir esse valor:
Vamos começar a substituir todos os valores que descobrimos e que nos deram no enunciado:
Ele já nos deu no enunciado que o valor do seno de 52° é igual a:
Substituindo na equação:
Passo 3
Agora é resolver a conta e correr pro abraço:
Multiplicando as duas primeiras parcelas:
Multiplicando a parcela resultante com a próxima:
Fazendo a última multiplicação:
Chegamos na primeira resposta que pede o módulo da força magnética!
Vamos para o próximo item!
Passo 4
Agora vamos calcular a aceleração da partícula. Para isso, vamos usar a Segunda Lei de Newton e a força que calculamos no último item. A Segunda Lei de Newton nos diz que a força é a multiplicação entre a massa e a aceleração:
Qual é a nossa força? A força magnética que calculamos no último item:
Quem é a massa da partícula? O que nos foi dada no enunciado, vou buscar pra você:
E a aceleração é o que gostaríamos de descobrir:
Então vamos substituir na equação:
Para encontrar , vamos dividir a força pela massa:
Quando dividimos duas potências de mesma base, nós mantemos a base e subtraímos os expoentes:
Então:
Terminando a divisão, temos:
Chegamos ao valor da aceleração!
Passo 5
Agora para fechar com chave de ouro, ele nos pergunta no item c, se a velocidade da partícula aumenta, diminui ou permanece constante com essa força sendo aplicada.
Uma coisa que devemos lembrar da parte teórica é que a força magnética forma 90° com a velocidade da partícula, ou seja, não estão na mesma direção.
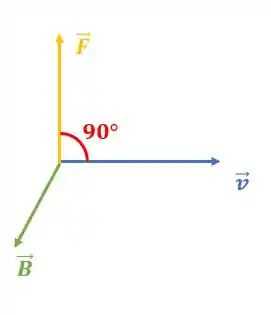
Dessa forma, a força não contribui para aumentar a velocidade, então a velocidade se mantém constante!
Resposta
- Constante