As propriedades magnéticas de materiais ferrosos já são conhecidas desde a Grécia antiga, onde já era conhecido um minério de ferro, a magnetita, que sendo um imã permanente, atrai pequenos fragmentos de ferro. Porém podemos também induzir campo magnético através de passagem de corrente por um fio condutor reto, da seção transversal circular. Se colocarmos uma carga puntiforme de teste, sobre a qual atua uma força magnética, temos que essa força terá:
- Vetor perpendicular à direção da velocidade da carga e do campo magnético induzido.
- Módulo inversamente proporcional ao da carga puntiforme inserida no campo magnético induzido.
- Vetor perpendicular ao campo magnético induzido e paralelo à direção da velocidade da carga.
- Vetor paralelo ao campo magnético induzido e perpendicular à direção da velocidade da carga.
- Módulo inversamente proporcional ao campo elétrico.
Passo 1
Tudo bem, ele me fala no enunciado que tem um campo Magnético induzido, porque uma corrente percorre um fio. Depois disso, ele colocou uma carga de testes e criou uma força magnética que atua sobre a carga de teste.
Agora ele quer saber o que sabemos dizer sobre esse vetor .
Primeira coisa que devemos nos lembrar é da fórmula para encontrar essa força magnética:
Ou seja, dependemos da carga , da velocidade dessa carga multiplicando vetorialmente o outro vetor de campo magnético .
Passo 2
Pensando só nesse produto vetorial entre a velocidade da carga e o campo magnético:
O vetor resultado desse produto sempre será perpendicular a esses dois vetores que se multiplicam, ou seja, forma com a direção do vetor velocidade e forma com a direção do vetor campo magnético:
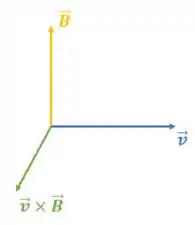
Se multiplicamos esse novo vetor criado pelo valor da carga que é um valor escalar, vamos manter a mesma direção, então, sabemos que a força magnética tem essa direção também, veja:
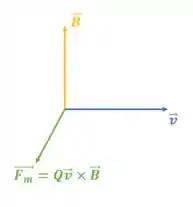
Entendemos que o vetor força magnética é perpendicular (forma 90°) à direção da velocidade e do campo magnético .
Ou seja, a primeira afirmação é a correta!
Passo 3
Mas vamos continuar analisando as outras respostas para aprender mais ainda!
Na segunda opção, ele afirma, que o módulo da força magnética é inversamente proporcional ao da carga puntiforme, porém olhando a fórmula:
Vemos que o módulo da força magnética:
Está diretamente ligado ao valor da carga. Então essa afirmativa é falsa.
Passo 4
A próxima opção diz que o vetor de força magnética é perpendicular ao campo magnético e paralelo à direção da velocidade, vamos olhar pro desenho do que ele está propondo:
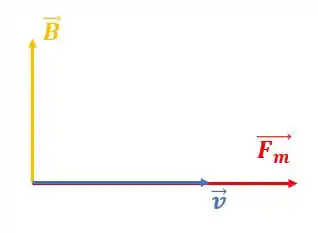
Completamente errado, né pessoal? Já falamos que o correto na primeira opção pela questão do produto vetorial :
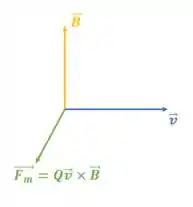
Passo 5
Essa próxima opção, o vetor força magnética é paralelo ao campo magnético induzido e perpendicular à direção da velocidade da carga é similar a anterior, olha o desenho:
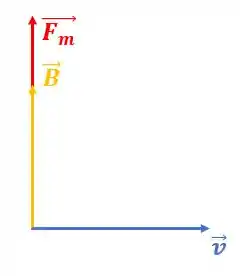
E também está ERRADO! Lembra sempre da figura do primeira opção!
Passo 6
Analisando a última opção temos: o módulo da força magnética é inversamente proporcional ao campo elétrico.
Pessoal, de onde ele tirou isso de campo elétrico? A força magnética nem depende do campo elétrico , e sim, do campo magnético .
Não fica com medo e pode afirmar com convicção que essa opção está erradíssima!
Resposta
Letra A: Vetor perpendicular à direção da velocidade da carga e do campo magnético induzido