Considere o circuito RC abaixo:
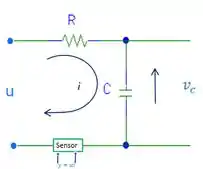
Onde , , a constante do sensor equivale a e é a corrente elétrica.
A entrada do sistema RC é uma tensão e a saída é . Quando desconsideramos o sensor, e a função de transferência do sistema é:
Quando o sensor é levado em consideração, e a função de transferência se torna:
Usando o SIMULINK, construa o diagrama de blocos em malha fechada do circuito RC para e e simule a resposta ao degrau para as duas malhas.
Passo 1
Neste exercício, construiremos dois diagramas de blocos em um mesmo arquivo do SIMULINK, para compararmos as respostas ao degrau. Um diagrama terá como função de transferência e o outro, .
Ambos os diagramas terão:
- Uma entrada, que será um bloco “Step”, simulando um degrau;
- Um bloco “Sum” para construirmos o sistema em malha fechada;
- Um bloco “Transfer Fcn” para entrarmos com a função de transferência.
A saída de ambos os diagramas será um bloco “Scope”, cujas propriedades alteraremos para ter os gráficos da resposta de e na mesma janela. Dessa forma, poderemos compará-los.
Passo 2
Vamos começar inserindo as entradas dos dois diagramas de blocos. Em um novo modelo no SIMULINK, insira dois blocos “Step”, um em cima do outro:

Em seguida, insira dois blocos “Sum”, um para cada sistema em malha fechada. Você encontrará esse bloco na biblioteca “Math Operations”:
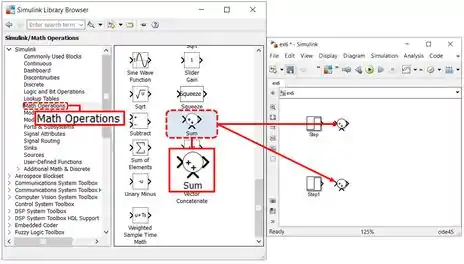
O bloco “Sum” tem duas entradas e uma saída. Por padrão, o “Sum” soma dois sinais de entrada e o resultado é dado pela saída do bloco. A soma dos dois sinais é indicada pelo sinal de de cada entrada.
Em uma malha fechada, fazemos a diferença entre um sinal de referência (no caso, o bloco “Step”) e o resultado da multiplicação entre esse sinal de referência e uma função de transferência (o sinal que sairá dos blocos “Transfer Fcn” representando e , como veremos mais pra frente).
Por isso, temos que alterar os parâmetros do bloco. Dê um duplo-clique em um dos blocos “Sum” e mude a propriedade a “List of signs”, destacada em vermelho abaixo:
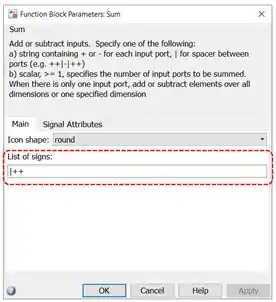
Para que seja feita a subtração de sinais, troque o por . Clique em “OK” e faça o mesmo procedimento para o outro “Sum”. Você verá que os sinais dos blocos mudaram:
Passo 3
O próximo passo é inserir e no modelo. Vamos fazer com que o diagrama de blocos de cima represente o circuito RC sem sensor, isto é, o diagrama de blocos de cima terá como função de transferência . Já o diagrama de blocos que ficará embaixo representará o circuito com sensor, ou seja, a função de transferência será .
Vamos começar por : vá à biblioteca “Continuous” e arraste um bloco “Transfer Fcn” para o modelo, alinhado com o “Step” e o “Sum” da parte de cima:
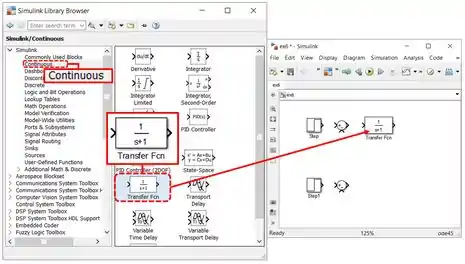
Para definir , dê um duplo-clique sobre o bloco “Transfer Fcn” que você acabou de incluir no modelo para acessar seus parâmetros. Vamos mexer nos parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).

Esses parâmetros recebem vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. No “Numerator coefficients”, o vetor tem os coeficientes do polinômio do numerador de . Já o vetor “Denominator coefficients” contém os coeficientes do polinômio do denominador de .
O numerador de é , logo, não precisamos mudar o do campo destacado em vermelho.
O polinômio do denominador é . Logo, também não precisamos alterar o campo destacado em azul, pois o vetor de coeficientes coincide com o padrão: .
Simplesmente clique em “OK”. Vamos construir o diagrama de blocos do circuito RC com sensor.
Passo 4
Insira um novo bloco “Transfer Fcn”, alinhado com os blocos “Step” e “Sum” de baixo:
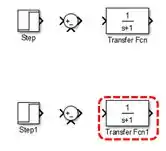
Altere os parâmetros “Numerator coefficients” e “Denominator coefficients” do bloco que você acabou de inserir, atualizando os vetores com os coeficientes dos polinômios do numerador e do denominador de .
O numerador de é , logo, devemos trocar o do campo “Numerator coefficients” por .
O polinômio do denominador é igual ao de : . Logo, não precisamos alterar o campo “Denominator coefficients”, pois, novamente, o vetor de coeficientes coincide com o padrão: .
Dessa forma, os parâmetros “Numerator coefficients” e “Denominator coefficients” de ficam assim:
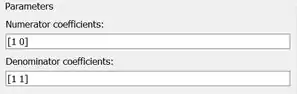
Clique em “OK” para registrar as alterações. Por enquanto, o modelo está assim:

Passo 5
Vamos inserir um bloco “Scope” para ser a saída de ambos os diagramas de blocos:
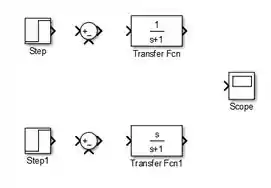
Precisamos que o “Scope” tenha duas entradas em vez de uma, para termos dois gráficos em uma mesma janela. Para isto, dê dois-cliques sobre o “Scope” para abrir sua janela e ter acesso aos seus parâmetros. Em seguida, clique na engrenagem destacada abaixo para abrir a janela com as propriedades do “Scope”.

Na aba “General” em “Scope parameters”, altere a propriedade “Number of axes” (destacada na imagem abaixo) de para e clique em “OK”. A janela do “Scope” ganhará mais um gráficos, como na imagem abaixo.
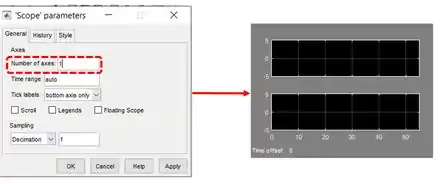
Feche a janela do “Scope” e veja que o bloco “Scope” ganhou uma setinha de entrada a mais:

Conecte os blocos como se fosse uma malha aberta, conectando a saída da “Transfer Fcn” com ) na entrada superior de “Scope” e a saída de “Transfer Fcn” com ), na entrada inferior de “Scope”:
Passo 6
Vamos fechar as malhas de ambos os diagramas. Para cada um deles, clique sobre a entrada de “Sum” que tem o sinal de menos e arraste, para surgir uma flecha vermelha tracejada. Conecte a extremidade “solta” dessa flecha na linha entre o bloco “Transfer Fcn” e o “Scope”, para criar um ponto de derivação:
Voilà! Modelo pronto! Agora é rodar a simulação, gerar os gráficos e ver as diferenças entre eles.
Resposta
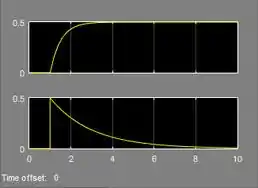
O gráfico de cima representa a resposta ao degrau do circuito RC desconsiderando o sensor. Já o gráfico de baixo é a resposta ao degrau considerando o sensor.