O diagrama abaixo apresenta um sistema em malha fechada onde na realimentação existe um ganho :
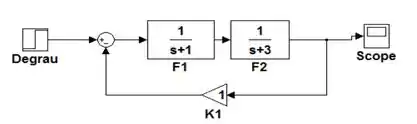
Usando o SIMULINK, encontre o limite de de tal forma que a resposta no tempo em malha fechada se mantenha estável.
Passo 1
Neste exercício, reproduziremos o diagrama de blocos do enunciado no SIMULINK. Logo, o modelo terá seis blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau;
- Um bloco “Sum” para construirmos o sistema em malha fechada;
- Dois blocos “Transfer Fcn” para as funções de transferência e ;
- Um bloco “Gain” para entrarmos com o ganho ;
- A saída do modelo será um bloco “Scope”, para gerar o gráfico da resposta ao degrau.
Para encontrarmos o limite de , vamos ajustar o valor do bloco “Gain” até que o sistema se estabilize. A cada mudança de valor, rodaremos a simulação e usaremos o “Scope” para ver o gráfico da resposta ao degrau. Quando a resposta se tornar instável, encontraremos o limite de .
Passo 2
Em um modelo novo, insira um bloco “Step”. O enunciado não detalhou as propriedades do degrau, por isso vamos usar os parâmetros padrão do bloco.
Ao lado do bloco “Step”, insira um bloco “Sum”, para iniciar o sistema em malha fechada. Você encontrará esse bloco na biblioteca “Math Operations”:
Por padrão, as duas entradas de “Sum” tem um sinal de , indicando que o bloco vai somar os dois sinais de entrada. Em uma malha fechada, usamos o bloco “Sum” para subtrair dois sinais. Por isso, devemos alterar o parâmetro “List of signs” do bloco, destacado em vermelho abaixo. Dê um duplo-clique sobre “Sum” para acessá-lo:

Para que seja feita a subtração de sinais, troque por no campo destacado em vermelho e clique em “OK”.
Passo 3
O próximo passo é inserir as duas funções de transferência no modelo. Vá à biblioteca “Continuous” e arraste dois blocos “Transfer Fcn” para o modelo, colocando-os em série, como na imagem abaixo:

Note que o bloco “Tranfer Fcn” mais à esquerda, representando , já é igual ao bloco que está na mesma posição no enunciado. Logo, não precisamos mexer em seus parâmetros e podemos partir para definir .
Dê um duplo-clique sobre o bloco “Transfer Fcn” mais à direita, que representará , para alterar os parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).
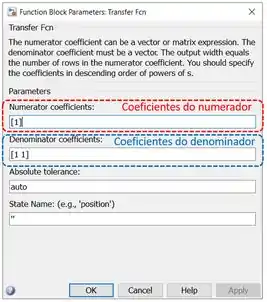
Em ambos os campos destacados, entramos vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. No “Numerator coefficients”, o vetor tem os coeficientes do numerador de . Já o vetor “Denominator coefficients” contém os coeficientes do denominador de .
O numerador de é , logo, não precisamos mudar o padrão de do campo destacado em vermelho.
O polinômio do denominador de é , logo, troque por no parâmetro “Denominator coefficients”:
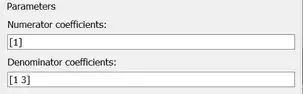
Por enquanto, o diagrama de blocos está com essa cara:
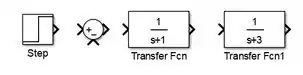
Passo 4
Insira um bloco “Scope”, alinhado com os blocos anteriores, para gerar o gráfico da resposta ao degrau. Em seguida, conecte os blocos, como se fosse uma malha aberta:

Lembrando que o bloco “Step” deve se conectar à entrada com o do bloco “Sum”, já que é o sinal de referência da malha fechada.
Vamos adicionar ao diagrama o bloco que falta: o bloco “Gain”, pertencente à biblioteca “Math Operations”:
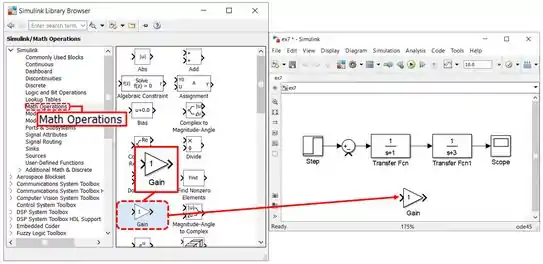
O bloco “Gain” tem uma entrada e uma saída. A entrada de “Gain”deve se conectar à saída de . Já a saída de “Gain” deve se conectar à entrada de “Sum” que tem o sinal , conforme a figura do enunciado.
Dica para deixar o diagrama mais organizado: podemos girar em um bloco no SIMULINK ao selecioná-lo e apertar Ctrl+R. Vamos fazer isso com o “Gain”, para ele ficar igualzinho ao diagrama no enunciado. Você vai acabar tendo que apertar Ctrl+R duas vezes para que o diagrama fique assim:

Bora fechar a malha? Conecte a saída de “Gain” à entrada de “Sum” restante:

Em seguida, clique sobre a entrada de “Gain” e arraste, para aparecer a flecha vermelha tracejada cuja extremidade “solta” você conectará na linha entre o bloco com e o “Scope”:
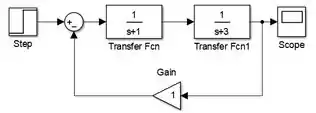
O diagrama de blocos está pronto!
Passo 5
Agora temos que ir ajustando o valor de “Gain”, que representa , para encontrarmos o valor máximo (ou mínimo) que pode assumir sem que o sistema se torne instável. Vamos começar com mesmo, que é o valor padrão (como podemos ver no diagrama que fizemos no SIMULINK).
Rode a simulação com o diagrama como ele está e veja o gráfico com a resposta:
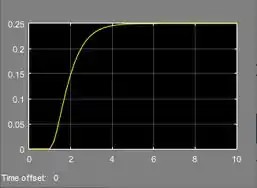
A resposta está bem estável, podemos alterar o valor de . Para isto, dê um duplo-clique sobre “Gain” e mude valor do parâmetro “Gain”, destacado em vermelho abaixo:
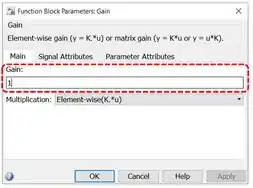
Vamos tentar usar valores maiores de . Troque por e veja que o “Gain” assumiu um novo valor no diagrama de blocos:

Rode a simulação novamente para ver o novo gráfico:
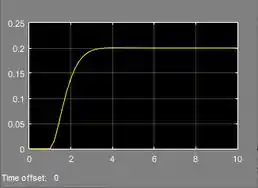
A resposta continua estável. Você pode continuar aumentando e verá que esse comportamento não muda: a resposta continuará estável.
Passo 6
Outra alternativa é diminuir , fazendo com que ele assuma valores negativos. Se você fizer , você terá:

Opa! A resposta não está mais parecida com o degrau, está parecendo uma rampa! Isso indica que estamos no limite da estabilidade. Se fizermos , por exemplo, , teremos:

Note que para , a resposta cresce indefinidamente e não se estabiliza, como podemos ver nos gráficos. Logo, deve ser maior que para que o sistema se mantenha estável.
Resposta
Para que o sistema se mantenha estável, .