Considere o sistema massa-mola-amortecedor (MMA) abaixo:
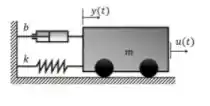
O corpo tem massa , o coeficiente de amortecimento é e a constante elástica da mola equivale a .
Considerando as condições iniciais nulas, o sistema tem a seguinte função de transferência:
No SIMULINK, gere o gráfico da resposta do sistema ao degrau unitário, executando uma simulação de .
Passo 1
Para vermos a resposta ao degrau unitário do sistema MMA, criaremos um modelo no SIMULINK com três blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau unitário;
- A função de transferência será incluída no modelo por meio do bloco “Transfer Fcn”;
- A saída do modelo será um bloco “Scope”, que mostrará a resposta do sistema MMA ao degrau unitário.
Precisaremos aumentar o tempo padrão de simulação de para e outros parâmetros de simulação para melhorar a resolução do gráfico da resposta do sistema MMA, produzido por “Scope”.
Passo 2
Vamos começar inserindo a entrada do modelo, que é um degrau unitário, em um novo modelo. Na biblioteca “Sources” do SIMULINK, encontre o bloco “Step” e arraste-o para o modelo em branco.
O bloco “Step” por padrão é um degrau unitário que se inicia a partir de Como o enunciado não especificou o instante em que o degrau começa, usaremos as propriedades padrão do bloco “Step” na simulação. Por isso, não precisamos acessar seus parâmetros e já podemos definir no modelo.
Vá à biblioteca “Continuous”, encontre o bloco “Transfer Fcn” e arraste-o para o modelo:
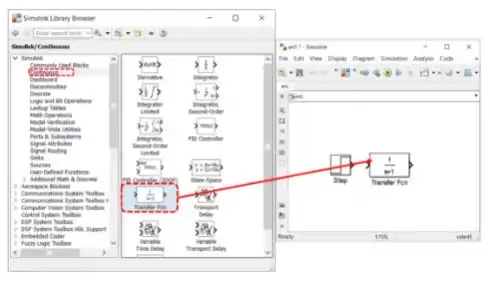
Vamos acessar os parâmetros do bloco “Transfer Fcn” que acabamos de inserir para definir , clicando duas vezes sobre ele:
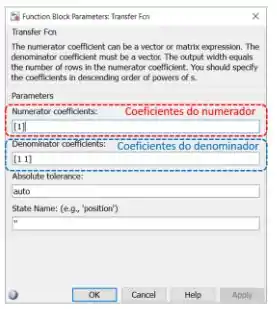
é definida alterando os dois parâmetros destacados acima. No campo destacado em vermelho, “Numerator coefficients”, devemos entrar um vetor com os coeficientes do polinômio do numerador de , indo do elemento do polinômio de maior ordem ao de menor ordem.
O polinômio do numerador de é , por isso, substitua por no campo destacado em vermelho.
No campo destacado em azul, “Denominator coefficients”, também devemos entrar um vetor, mas desta vez com os coeficientes do polinômio do denominador, indo do elemento de maior expoente ao de menor expoente.
O polinômio do denominador é , logo, o vetor a ser entrado no campo destacado em azul é .
Logo, os parâmetros “Numerator coefficients” e “Denominator coefficients” deverão ficar assim:
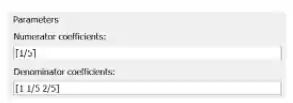
Clique em “OK” e você verá que o bloco “Transfer Fcn” mudou de cara:
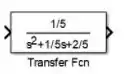
Ele agora contém em seu interior.
Passo 3
Agora vamos incluir a saída do modelo, um bloco “Scope”, que nos apresentará a resposta do sistema MMA ao degrau unitário. Vá a biblioteca “Sinks”, arraste para o modelo um bloco “Scope” e conecte os três blocos entre si. O modelo ficará assim:

A modelagem do sistema MMA está pronta! Antes de rodar o programa, precisamos ajustar o tempo de simulação de para . Na barra superior da janela do modelo, no campo onde podemos alterar o tempo de duração da simulação, destacado abaixo, troque por :
Execute a simulação e veja como ficou o gráfico, já ajustando sua escala, usando o botão “Autoscale” destacado abaixo, para ele ocupar toda a janela:

Passo 4
Note que a curva está meio pontiaguda. Para deixá-la mais “redondinha”, acesso os parâmetros de simulação, clicando sobre a engrenagem da barra superior da janela onde construímos os modelos, destacada em vermelho abaixo:

Na seção “Solver” da janela “Configuration Parameters”, estão os parâmetros de tamanho mínimo e máximo do passo do algoritmo da simulação (destacados em vermelho abaixo), que devem ser ajustados para deixar a curva mais redonda:
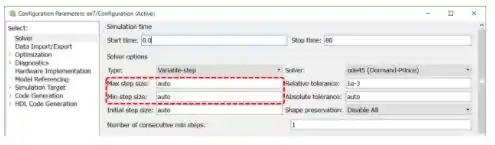
Os parâmetros “Max step size” (tamanho máximo de passo) e “Min step size” (tamanho mínimo de passo) são calculados automaticamente por padrão. Para termos curvas com maior resolução, isto é, mais “redondinhas”, devemos usar valores de passo bem pequenos, da ordem de . Eu adotei os valores abaixo, mas você pode usar os valores que quiser.

Clique em “OK”, feche a janela do “Scope” e rode a simulação de novo. Você verá que uma parte do gráfico “sumiu”, indicando que ocorreu o fenômeno de “amnésia”:
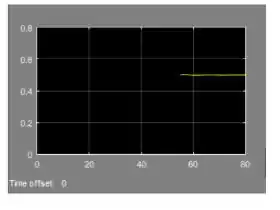
Passo 5
Para corrigir a amnésia, devemos mudar a propriedade “Limit data points to last” do bloco “Scope”.
Para acessar as propriedades de “Scope”, na janela do gráfico com um pedaço faltando, clique na engrenagem destacada abaixo. Uma janela chamada “Scope parameters” se abrirá. Vá na aba “History”, onde tem a propriedade “Limit data points to last”, destacada abaixo:
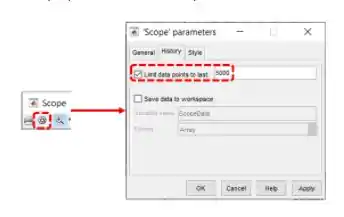
Vamos aumentar o valor do campo destacado em vermelho para corrigir a amnésia. Vamos mudar esse valor para , fechar a janela do “Scope” e executar a simulação de novo.
Quando você abrir o gráfico de novo, você verá que a curva vai estar completinha e bem bonitinha =)
Resposta
