O tanque de nível abaixo está sob influência de perturbações degrau nas vazões de alimentação e :
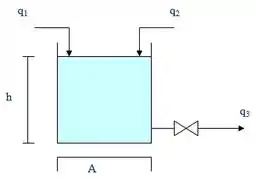
Onde é o nível da água e é a seção transversal do tanque, que tem um diâmetro . A vazão de saída é representada por e é controlada por uma válvula que atua sob uma resistência linear de .
A função de transferência que relaciona o nível da água à vazão de entrada é:
A função de transferência que relaciona o nível da água à vazão de entrada é igual a :
O nível é dado pela soma:
Considere que é um degrau de que se inicia em e que também é um degrau de , mas que se inicia em .
Usando o SIMULINK e considerando que o tanque está vazio em , determine o nível do tanque após .
Passo 1
O tanque é um sistema com duas entradas ( e ) e uma saída (o nível ). Para unirmos essas duas entradas e obtermos uma única saída, usaremos o bloco “Sum”.
Cada entrada tem sua própria função de transferência, resultando em um modelo com seis blocos:
- O sistema tem duas entradas, ambas degraus. Por isso, o modelo terá dois blocos “Step”. Contudo, eles terão parâmetros diferentes entre si, pois o degrau que representa inicia em e o outro, representando , em ;
- Cada uma das entradas será multiplicada por sua respectiva função de transferência, logo, o modelo terá dois blocos “Transfer Fcn”, um para e outro para ;
- As saídas dos blocos “Transfer Fcn” serão somadas por um bloco “Sum”;
- A saída do sistema será um bloco “Scope”, que os dará o gráfico de .
O enunciado pede para que simulemos o tanque por , dessa forma, podemos ver bem o impacto de sobre , quando ele se inicia em .
Um detalhe importante é que, como as unidades das grandezas do exercício estão em minutos, não precisamos fazer conversão alguma de minutos para segundos, que á a unidade de tempo que estamos acostumados a trabalhar no SIMULINK.
Passo 2
Vamos começar pelas entradas do sistema. Em um modelo do SIMULINK novo, insira dois blocos “Step” e alinhe-os verticalmente:

Precisamos alterar as propriedades deles, para que eles tenham as características de e dadas no enunciado.
Vamos dizer que o bloco de cima é , que é um degrau de amplitude de e se inicia em . Clique duas vezes no “Step” de cima para ter acesso a seus parâmetros:

Os parâmetros que devemos olhar são o “Step time”, destacado em vermelho acima, e os parâmetros “Initial value” e “Final value”, destacos dentro de um mesmo retângulo azul.
O “Step time” é o instante quando o degrau ocorre. Por padrão, ele é igual a . Como queremos que ocorra no instante , devemos alterar esse campo de para .
O parâmetro “Initial value” representa a amplitude do sinal antes que o degrau ocorra e por padrão é igual a . Vamos deixá-lo igual a pois o tanque deve estar vazio no começo da simulação.
O parâmetro “Final value” representar o valor do sinal após a ocorrência do degrau. Isso quer dizer que a diferença entre “Final value” e “Initial value” dá a amplitude do degrau. Por padrão, “Final value” é igual a . Como é um degrau de amplitude de , não precisamos alterar o valor padrão.
No final, os parâmetros do degrau representando ficam assim.

Clique em “OK” para registrar as mudanças e dê um duplo-clique no bloco “Step” de baixo do modelo, para definir . Lembrando que também é um degrau de , mas que se inicia em .
Devemos verificar os mesmos três parâmetros que verificamos no outro bloco “Step”: “Step time”, “Initial value” e “Final value”.
Como começa em , devemos alterar o “Step time” para . Já os parâmetros “Initial value” e “Final value” não precisam ser alterados, pelas mesmas razões que não mudamos seus valores padrão no bloco de cima.
No final, os parâmetros do bloco “Step” representando ficam assim:

Clique em “OK” para registrar as mudanças e fechar a janela de parâmetros.
Passo 3
Após inserirmos os blocos “Step” no modelo, devemos entrar com as funções de transferência e . Vá à biblioteca “Continuous” e arraste um bloco “Transfer Fcn” para o modelo:

Vamos inserir somente um bloco “Transfer Fcn”, pois basta definir com este bloco e em seguida copiá-lo e colá-lo para definir , já que e são iguais.
Dê um duplo-clique sobre o bloco “Transfer Fcn” que você acabou de incluir no modelo para ter acesso a suas propriedades:
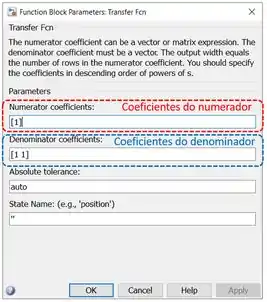
Para definir , vamos alterar os parâmetros “Numerator coefficients” (destacado em vermelho acima) e “Denominator coefficients” (destacado em azul). Ambos os parâmetros têm como entrada vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. No caso de “Numerator coefficients”, são os coeficientes do polinômio do numerador da função de transferência. Já o vetor “Denominator coefficients” deve conter os coeficientes do polinômio do denominador da função de transferência.
O numerador de é , logo, devemos trocar o do campo destacado em vermelho por .
O polinômio do denominador é , onde é a área de seção transversal do tanque, que tem diâmetro . A área é a área de um círculo, que é calculada como:
Como , temos . Logo, o vetor a ser entrado no campo destacado em azul é .
No final, os parâmetros “Numerator coefficients” e “Denominator coefficients” de ficarão assim:
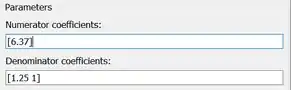
Clique em “OK” para registrar os novos parâmetros e fechar a janela de parâmetros de “Transfer Fcn”.
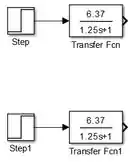
Com definido, como é igual a , você pode clicar no bloco “Transfer Fcn” que você acabou de alterar e dar um Ctrl+C para copiá-lo e um Ctrl+V para colá-lo no mesmo modelo. Desta forma, você terá dois bloquinhos iguais.
Aproveite para conectar cada bloco “Step” a uma entrada de um bloco “Transfer Fcn”. O modelo está assim, por enquanto:
Passo 4
Agora é hora de adicionarmos o bloco “Sum” para somarmos as saídas dos blocos “Transfer Fcn”! Vá à biblioteca “Math Operations”, encontre o bloco “Sum” e arraste-o para o modelo:

O bloco “Sum” por padrão tem duas entradas, cada uma com um sinal de . Isso indica que o “Sum” vai somar dois sinais de entrada e vai dar o resultado na sua saída. Como queremos somar dois sinais ( e ), não precisamos alterar as propriedades padrão de “Sum”.
Conecte a saída de cada bloco “Transfer Fcn” a um entrada de “Sum”. Desta forma, seu modelo ficará assim:
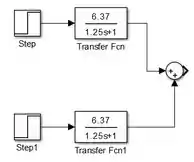
Passo 5
Para finalizar, vamos inserir a saída do modelo: um bloco “Scope”. Encontre-o na biblioteca “Sinks”, arraste-o para o modelo e conecte a sua entrada à saída do bloco “Sum”:
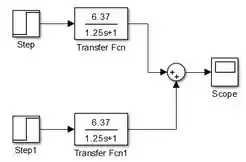
Modelo pronto! Falta só ajustar o tempo de simulação de (padrão do SIMULINK) para , no campo destacado abaixo:
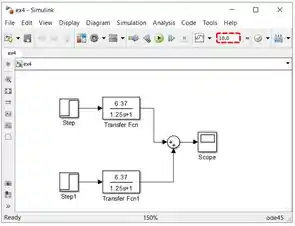
Execute a simulação e veja como ficou o gráfico. Já ajuste sua escala, usando o botão “Autoscale”, para ele ocupar toda a janela:

Passo 6
Para ver o nivel do tanque, vamos usar uma ferramenta que nos dá as coordenadas dos pontos do gráfico. Na barra de ferramentas da janela do “Scope”, onde temos o gráfico do nível do tanque, clique em “Try Time Scope”, indicado abaixo:
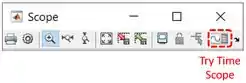
Aparecerão ferramentas novas para analisar o gráfico. Para vermos as coordenadas da curva, clique no botão “Cursor Measurements” com o ícone de uma régua, destacado abaixo:

Aparecerão duas retas verticais no gráfico, com bolinhas onde elas interceptam a curva, e uma janela à direita, indicando as coordenadas dessas bolinhas:

As retas são identificadas como e e na janela à direita, temos as coordenadas de tempo (eixo horizontal do gráfico) e nível (eixo vertical) da intersecção delas com a curva.
Clique na reta mais à direita, identificada como , e arraste-a até o final do gráfico. Você terá essas coordenadas:
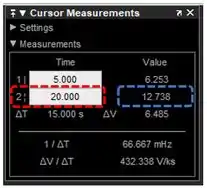
Destacado em vermelho, temos a coordenadas de tempo da reta e, em azul, temos a coordenada do eixo vertical da intersecção da reta com a curva. A coordenada de tempo é , logo, a coordenada do eixo vertical é o nível do tanque depois de . Desta forma, a resposta do exercício é a coordenada destacada em azul: o nível do tanque após é .
Resposta
O nível do tanque após é .