Considere o motor DC abaixo:

Ele tem como entrada a tensão e como saída, o ângulo . Considerando as constantes:

• Momento de inércia do motor e carga: ;
• Coeficiente de atrito do motor e carga: ;
• Resistência de armadura: ;
• Indutância da armadura: ;
• Constante elétrica: ;
• Constante de torque: .

Considerando as condições iniciais nulas, o motor DC tem como função de transferência:

Usando o SIMULINK, simule a resposta ao degrau em um sistema em malha fechada.

Em novo modelo do SIMULINK, insira um bloco “Step”, que servirá como entrada no nosso modelo. Como o enunciado não deu maiores especificações sobre o degrau, não vamos alterar as propriedades de “Step”.

Em seguida, insira um bloco “Sum”, para começarmos a construir o sistema em malha fechada. Você encontrará esse bloco na biblioteca “Math Operations”:

O bloco “Sum” tem duas entradas e uma saída. Por padrão, cada entrada tem um sinal de , indicando que o “Sum” vai somar dois sinais de entrada e a soma será fornecida pela saída do bloco. Contudo, em uma malha fechada, fazemos a subtração entre um sinal de referência (no caso, nosso bloco “Step”) e o resultado do produto entre esse sinal de referência e uma função de transferência (o sinal que sairá do bloco “Transfer Fcn” representando , como veremos mais pra frente).

Logo, temos que alterar os parâmetros do bloco. Dê um duplo-clique sobre “Sum” para acessar seus parâmetros. A propriedade que vamos alterar é a “List of signs”, destacada em vermelho abaixo:

Como o padrão do “Sum” é somar dois sinais, no campo “List of signs” temos . Para que seja feita a subtração de sinais, troque por . Clique em “OK” e você verá que o bloco vai ter esses sinais em seu interior:

O próximo passo é inserir no modelo. Vá à biblioteca “Continuous” e arraste um bloco “Transfer Fcn” para o modelo:

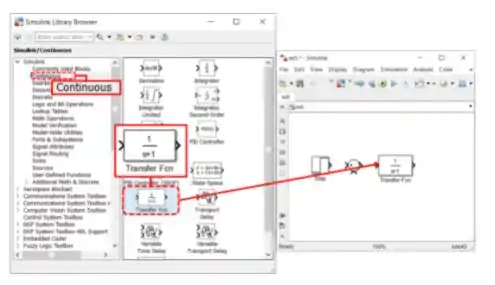
Para definir , dê um duplo-clique sobre o bloco “Transfer Fcn” que você acabou de incluir no modelo para ter acesso a seus parâmetros. Vamos mexer nos parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).

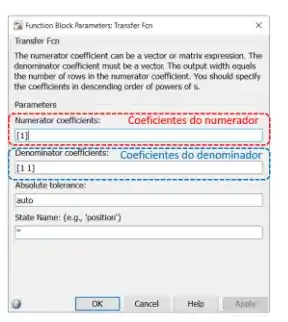
Entramos vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente, em ambos os parâmetros. No “Numerator coefficients”, o vetor tem os coeficientes do polinômio do numerador de . Já o vetor “Denominator coefficients” contém os coeficientes do polinômio do denominador de .

O numerador de é , logo, devemos trocar o do campo destacado em vermelho por .

O polinômio do denominador é . Considerando as constantes dadas no enunciado, temos:

Logo, o vetor a ser entrado no campo destacado em azul é:

Portanto, os parâmetros “Numerator coefficients” e “Denominator coefficients” de ficarão assim:

Clique em “OK” para registrar as mudanças e fechar automaticamente a janela com os parâmetros. Você notará que o bloco “Transfer Fcn” tem agora em seu interior. Aumente o tamanho do bloco, selecionando-o e arrastando um dos seus cantos. Dessa forma, você conseguirá ver por completo. Por enquanto, nosso modelo está assim:

Vamos inserir a saída do modelo: um bloco “Scope”, para vermos o gráfico da resposta ao degrau do motor DC. Após adicionar o bloco “Scope”, conecte os blocos, primeiramente como se fosse uma malha aberta:

Para fechar a malha, clique sobre a entrada de “Sum” que tem o sinal de menos e arraste. Aparecerá uma flecha vermelha tracejada. Conecte a extremidade “solta” dessa flecha na linha entre o bloco com e o “Scope”, para criar um ponto de derivação:

Pronto! Temos o sistema em malha fechada e já podemos executar o programa, para ver a resposta ao degrau.

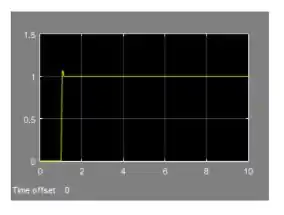
Após encerrar a execução, clique duas vezes sobre o “Scope” para ver o gráfico. Use o botão “Autoscale”, destacado abaixo, para ajustar a escala do gráfico.

Vixe, ele ficou bem esquisito.

O motivo de o gráfico ter ficado esquisito é que o número de dados calculados na simulação ultrapassou o limite padrão do bloco “Scope”. Para corrigir esse problema, temos que acessar as propriedades do bloco “Scope”, clicando na engrenagem destacada abaixo (que está na barra superior da janela do “Scope”), e mudar a propriedade “Limit data points to last”.

Ao clicar na engrenagem, o “Scope parameters” se abrirá. Vá à aba “History”, onde tem a propriedade “Limit data points to last”, destacada abaixo:

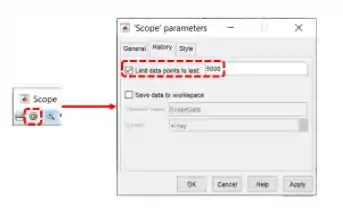
Desmarque a caixinha à esquerda, dentro do destaque em vermelho. Dessa forma, não haverá limite de dados e o gráfico ficará bonitão.

Clique em “OK” para registar a alteração, feche a janela do “Scope” e rode a simulação novamente. Ao abrir o gráfico, você verá que ele terá um formato que estamos mais acostumados a ver em exercícios de controle com entrada degrau.