Suponha que um controlador é projetado usando um modelo simples como:
O controlador pode não estar modelado precisamente. Existe um modelo alternativo:
- Plote as respostas ao degrau em malha aberta de e ;
- Plote as respostas ao degrau em malha fechada de e , com um controlador proporcional de ganho .
Utilize um tempo máximo de .
Passo 1
Neste exercício, criaremos em um mesmo arquivo do SIMULINK dois diagramas de bloco, um para e outro para . Na letra a, vamos construir os diagramas malha aberta para vermos a resposta ao degrau. Ambos os diagramas em malha aberta terão:
- Uma entrada simulando um degrau, que será um bloco “Step”;
- Um bloco “Transfer Fcn” para entrarmos com a função de transferência ( ou ).
A saída de ambos os diagramas será um bloco “Scope”, que faremos ter duas entradas para comparar a resposta ao degrau de e .
Para fazer a letra b, incluiremos um bloco “Sum” em ambos os diagramas que construímos na letra a para fechar as malhas. Incluiremos també um bloco “Gain” para fazer um controlador proporcional nas malhas fechadas.
Passo 2
Vamos começar construindo os diagramas em malha aberta. Em um novo modelo no SIMULINK, insira dois blocos “Step”, um em cima do outro:
![]()
O próximo passo é inserir e no modelo. Vamos fazer com que a função de transferência do diagrama de blocos de cima seja . Já o diagrama de blocos que ficará embaixo terá como função de transferência .
Vá à biblioteca “Continuous” e arraste dois blocos “Transfer Fcn” para o modelo:

Note que o bloco “Tranfer Fcn” de cima, que representará , já tem por padrão a função de tranferência igual a . Logo, não precisamos mexer mais nele e podemos já definir .
Dê um duplo-clique sobre o bloco “Transfer Fcn” de baixo, que representará , para mudar os parâmetros “Numerator coefficients” (destacado em vermelho abaixo) e “Denominator coefficients” (destacado em azul).
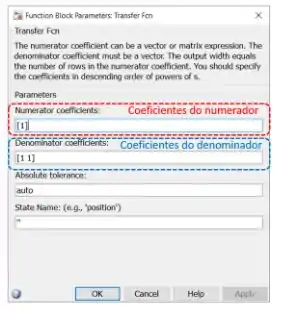
Em ambos os campos destacados, entramos vetores com coeficientes de polinômios, indo do elemento de maior expoente ao de menor expoente. “Numerator coefficients” receberá os coeficientes do numerador de e “Denominator coefficients”, os coeficientes do denominador de .
O numerador de é , logo, altere o do campo destacado em vermelho para .
O polinômio do denominador de é , logo, troque por no parâmetro “Denominator coefficients”.
Ao final, os parâmetros ficaram assim:
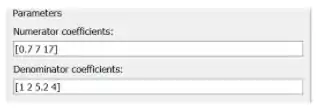
Clique em “OK” e aumente o bloco que contém , para ver a função de transferência por completo. Nosso modelo por enquanto está assim:
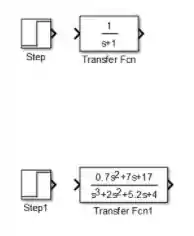
Passo 3
Vamos inserir um bloco “Scope” para ser a saída de ambos os diagramas:

Vamos adicionar mais uma entrada em “Scope”, para termos dois gráficos em uma mesma janela e podermos comparar as respostas. Para isto, dê dois-cliques sobre o “Scope” para abrir sua janela e clique na engrenagem destacada abaixo para acessar as propriedades do “Scope”.

Na aba “General” em “Scope parameters”, altere a propriedade “Number of axes” (destacada na imagem abaixo) de para e clique em “OK”.

Feche a janela do “Scope” e veja que o bloco “Scope” ganhou uma setinha de entrada a mais. Conecte os blocos de cada diagrama em série, como na imagem abaixo:
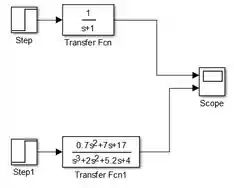
Da forma como os blocos estão conectados acima, a resposta ao degrau de estará no gráfico de cima da janela do “Scope”, e a resposta de , no gráfico de baixo.
O modelo da letra a está pronto e podemos rodar o programa. Não esqueça de alterar o tempo de simulação para . Você terá as seguintes respostas ao degrau:
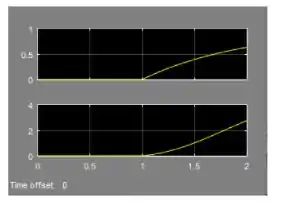
Desta forma, encerramos a letra a do exercício e podemos começar a fazer a letra b.
Passo 4
Para fazermos os diagramas de blocos da letra b, primeiro precisamos desconectar os blocos “Step” dos blocos “Transfer Fcn”, selecionando as flechas que os conectam e as deletando:
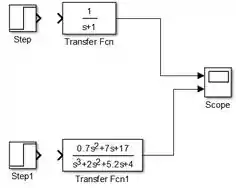
Em seguida, vamos inserir dois blocos “Sum”, um para cada sistema em malha fechada:

Devemos alterar as propriedades dos blocos “Sum”, para que eles façam a diferença entre o sinal de referência (o bloco “Step”) e o sinal de saída dos blocos “Transfer Fcn”. Desta forma, teremos dois diagramas em malha fechada.
Dê um duplo-clique em um dos blocos “Sum”, mude a propriedade a “List of signs” de para . Clique em “OK” e faça o mesmo procedimento para o outro “Sum”. O modelo ficará com essa cara:
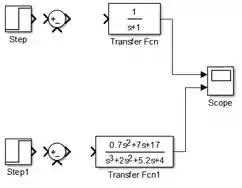
Passo 5
Para fazer o controlador proporcional, insira um bloco “Gain” entre o “Sum” e o “Transfer Fcn”, para cada diagrama de blocos, como na figura abaixo:

Precisamos alterar o valor dos blocos “Gain” para , pois foi pedido no enuciado. Dê um duplo-clique sobre cada um dos blocos “Gain” e mude valor do parâmetro “Gain” de para , no campo destacado abaixo:

Clique em “OK” para registrar as alterações e conecte os blocos de cada diagrama como se fosse uma malha aberta, como na imagem abaixo:
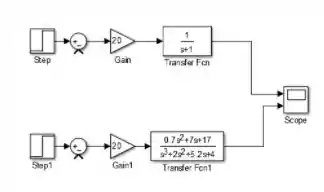
Passo 6
Vamos fechar as malhas de ambos os diagramas. Para cada um deles, clique sobre a entrada de “Sum” que tem o sinal , arraste para surgir a flecha vermelha tracejada e conecte a extremidade livre dessa flecha na linha entre o bloco “Transfer Fcn” e o “Scope”.
Pronto! Temos os diagramas em malha fechada com controlador proporcional exigidos pela letra b do exercício. Para vermos a resposta ao degrau, rode a simulação novamente:
Resposta
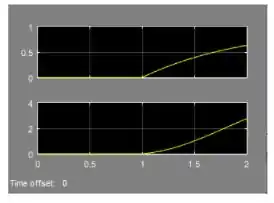
- As respostas ao degrau de e em malha aberta são:
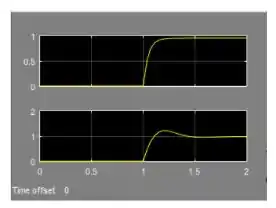
- As respostas ao degrau de e em malha fechada com um controlador proporcional com são:

Sendo que o gráfico superior é a resposta de e o inferior, de . Note que enquanto as respostas em malha aberta são bem diferente entre si, as respostas em malha fechada são muito parecidas.