Dada a função de transferência abaixo, que representa a dinâmica de um sistema que tem como entrada e saída :
No SIMULINK, esboce o gráfico de para uma entrada em degrau com amplitude .
Passo 1
Para plotarmos , usaremos o bloco “Transfer Fcn” para entrar com a função de transferência. Mas lembra como definimos uma função de transferência nesse bloco? Precisamos que o numerador e o denominador da função de transferência sejam poinômios, o que não é o caso do denominador, que tem dois termos entre parênteses que precisam ser multiplicados.
Para evitar a multiplicação dos termos, usaremos a operação de blocos em série, apresentada abaixo:

Nesta operação da álgebra de blocos, dois blocos em sequência, cada um com uma função de transferência e , equivalem a um único bloco cuja função de transferência é o produto entre e .
Contudo, usaremos essa operação no “sentido inverso”: vamos “quebrar” a função de transferência dada pelo enunciado em duas. Desta forma, não precisaremos multiplicar os termos do denominador para ter um polinômio só.
A função de transferência vai ser quebrada da seguinte forma:
Repare que se eu multiplicar por , eu tenho a função de transferência do enunciado.
Logo, nosso modelo no SIMULINK terá quatro blocos:
- A entrada do modelo será um bloco “Step”, simulando um degrau unitário;
- Dois blocos “Transfer Fcn”, uma para e outro para ;
- A saída do modelo será um bloco “Scope”, que mostrará a resposta ao degrau unitário.
Passo 2
Em um novo modelo do SIMULINK, insira um bloco “Step”, para simular a entrada , que é um degrau unitário.
Por padrão, o bloco “Step” é um degrau unitário que se inicia em Como o enunciado não especificou o instante em que o degrau começa, vamos deixar ele começando em mesmo. Desta forma, não precisamos alterar os parâmetros do bloco e podemos continuar a inserir blocos no modelo.
Vamos inserir um bloco “Transfer Fcn” para entrarmos com no modelo. Para isto, procure o bloco na biblioteca “Continuous” e arraste-o para o modelo:
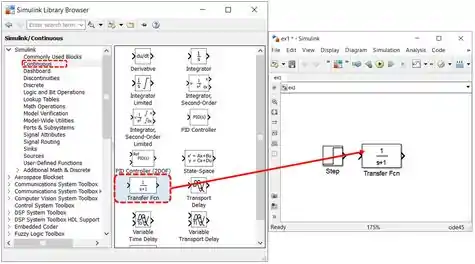
Precisamos acessar os parâmetros do bloco “Transfer Fcn” que acabamos de inserir para definir , clicando duas vezes sobre ele:
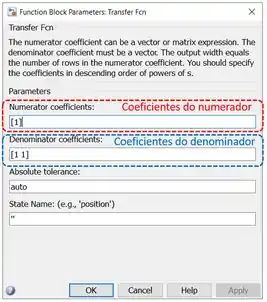
Uma função de transferência é definida alterando os dois parâmetros destacados acima. No parâmetro destacado em vermelho, “Numerator coefficients”, entramos com um vetor com os coeficientes do polinômio do numerador da função de transferência, indo do elemento do polinômio de maior ordem ao de menor ordem.
Já no parâmetro destacado em azul, “Denominator coefficients”, também entramos com um vetor, só que com os coeficientes do polinômio do denominador, indo do elemento de maior expoente ao de menor expoente.
O polinômio do numerador de é , por isso, substitua por no campo destacado em vermelho.
O polinômio do denominador é , logo, o vetor a ser entrado no campo destacado em azul é .
Portanto, os parâmetros “Numerator coefficients” e “Denominator coefficients” deverão ficar assim para :

Clique em “OK” e o bloco “Transfer Fcn” terá em seu interior:

Dica: se o polinômio for muito comprido, você pode aumentar o tamanho do bloco para ver a função de transferência inteira. Vá com o mouse sobre o bloco, clique em um dos cantos dele e arraste. Você verá que o bloco mudará de tamanho.
Passo 3
Insira um segundo bloco “Transfer Function” para entrar com e clique duas vezes sobre ele para transformá-lo em .
O numerador de é , igual ao valor padrão da propriedade “Numerator coefficients”, por isso, não precisamos alterar esse parâmetro.
O polinômio do denominador de é , logo, o vetor a ser entrado no campo da propriedade “Denominator coefficients” é .
Logo, os parâmetros de ficarão assim:
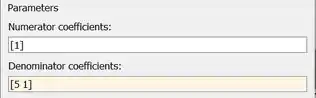
Clique em “OK” para salvar as alterações. Por enquanto, nosso modelinho está assim:

Passo 4
Falta adicionar o último bloco do modelo, que é a saída do sistema: um bloco “Scope”. Vá à biblioteca “Sinks” e arraste o “Scope” para o modelo. Em seguida, conecte os quatro blocos da seguinte forma:

É muito importante que os blocos “Transfer Fcn” sejam conectados em série, para termos a função de transferência do enunciado. Como o modelo acima é simples, conectá-los dessa forma pode parecer óbvio, mas é bom ter a operação dos blocos em série em mente quando estiver trabalhando com modelos maiores.
Com o modelo pronto, bora rodar a simulação! Quando a execução do programa terminar, dê um duplo-clique sobre “Scope” para ver o gráfico de . Não esqueça de ajustar a escala do gráfico clicando no botão “Autoscale”, na barra superior da janela do gráfico:
![]()
Resposta
