Considere os sistemas de primeira a quarta ordem dados por:
Plote em um mesmo gráfico as respostas ao degrau unitário de , , e e compare-as.
Passo 1
O exercício pede para plotarmos em um mesmo gráfico as resposta ao degrau unitário das funções de transferência , , e . Para isto, usaremos a função para criarmos as funções de transferência no MATLAB e, em seguida, usaremos a função , que plota a resposta ao degrau de uma função de transferência, para cada uma.
Passo 2
Primeiramente devemos criar , , e no MATLAB, usando a função , que tem como sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). Ambos os vetores vão do elemento com maior expoente ao de menor expoente.
retorna um objeto representando a função de transferência, que será armazenada em .
Vamos começar com , cujo numerador é . Já o denominador é o polinômio . Em um novo script, vamos criar duas variáveis contendo os coeficientes dos polinômios de . A primeira variável representará os coeficientes do polinômio do numerador e será chamada de . A segunda variável será um vetor chamado e terá os coeficientes do polinômio do denominador. Após criar as duas variáveis de entrada de , digite o comando :
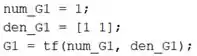
Desta forma, a função de transferência é criada e armazenada na variável Podemos ver como ficou, rodando o programa e imprimindo-o no Command Window:

Faça o mesmo procedimento para :

A variável contém o numerador de e o vetor contém os coeficientes do polinômio do denominador de . A função de transferência é criada usando e é armazenada na variável . Vamos ver como ficou :

Passo 3
Para criar , adicione em seu script o comando:
![]()
Execute o programa e veja como ficou :

Para definir , vamos criar uma “função de transferência auxiliar”, chamada de :
Temos então que
Vamos criar os vetores com os coeficientes dos polinômios do numerador e do denominador de . Vamos chamá-los de e . Logo em seguida, vamos criar usando a função :

Para calcular , adicione o comando:
![]()
Desta forma, tem essa cara:

Passo 4
Para plotar a resposta ao degrau unitário de , , e , usaremos o comando , que tem a sintaxe:
A função plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Para termos a resposta ao degrau unitário de , , e , devemos incluir no nosso script os comandos , e assim por diante. Contudo, o enunciado pediu que plotássemos tudo no mesmo gráfico. Para fazermos isto, devemos incluir o comando após o primeiro comando que digitarmos:
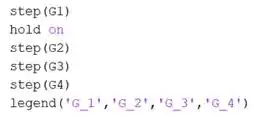
O comando faz com que a curva que acabou de ser plotada não seja substituída pela próxima a ser plotada, de forma que elas apareçam juntas no gráfico.
O comando serve para criar a legenda do gráfico, para sabermos qual é a resposta de cada função de transferência.
Execute o programa e você terá o gráfico com as respostas de , , e ao degrau unitário.
Resposta
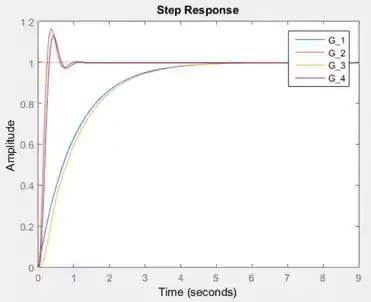
A curva azul é a resposta de ao degrau unitário.
A curva vermelha é a resposta de .
A curva amarela é a resposta de .
A curva roxa é a resposta de .
As respostas de e são similares, enquanto as respostas de e são parecidas.