Seja
Plote a resposta ao degrau de amplitude de .
Passo 1
O exercício pede para gerarmos o gráfico da resposta ao degrau de amplitude para uma função de transferência . Para isto, usaremos a função para criarmos no MATLAB e, em seguida, usaremos a função , que plota a resposta ao degrau de uma função de transferência.
Como é em função de e o enunciado não especifica mais nada, isso quer dizer que ela foi obtida por meio da transformada de Laplace a partir de funções no domínio de tempo contínuo.
Passo 2
Vamos relembrar a sintaxe da função :
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
Precisamos criar os vetores com os coeficientes dos polinômios, mas repare que o numerador e o denominador de estão fatorizados. Logo, precisamos expandi-los (isto é, multiplicar os termos) para termos uns polinômios bem bonitos para pegar os coeficientes.
Vamos fazer isso no MATLAB mesmo. Em um script, digite as linhas de código:

Na primeira linha, criamos uma variável simbólica .
Na segunda linha, entramos com o numerador de , armazenando-o na variável .
Na terceira linha, usamos o comando do MATLAB em . Este comando multiplicará os termos de e gerará o polinômio que precisamos, armazenando-o em .
Rodando o programa, temos:
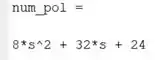
Adicione ao seu script as duas linhas de código abaixo, para fazer exatamente a mesma coisa com o denominador de :
![]()
Na primeira linha, entramos com denominado de , armazenando-o em . Em seguida, usamos em para gerar o polinômio do denominador, armazenando-o em .
Rodando o programa, temos os polinômios do numerador e do denominador de :

Passo 3
Agora que conhecemos os polinômios do numerador e do denominador de , podemos criar os vetores que servirão de entrada para .
O polinômio do numerador é . Já o polinômio do denominador é .
No nosso script, vamos criar dois vetores contendo os coeficientes dos polinômios. O primeiro vetor conterá os coeficientes do polinômio do numerador e será chamado de . O segundo vetor se chamará e terá os coeficientes do polinômio do denominador.
Ambos os vetores vão do elemento com maior expoente ( para o numerador e para o denominador) ao de menor expoente ( para o numerador e para o denominador, pois multiplicam ):
![]()
Em seguida, utilize a função para criar a função de transferência no MATLAB:
![]()
A função de transferência é armazenada na variável , isto é, é igual a .
Vamos ver a carinha dela? Rode o programa e você terá:

Passo 4
Agora que já entramos com no MATLAB, vamos ver qual é a resposta de a um degrau de amplitude . Para isto, usaremos a função , que tem a sintaxe:
A função com a sintaxe acima plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .
Se quiséssemos a resposta ao degrau unitário, bastaria incluir o comando em nosso código. Contudo, queremos ver a resposta para um degrau de amplitude . Por isso, devemos multiplicar por ao utilizarmos . Isto quer dizer que você deve adicionar no script o seguinte comando:
![]()
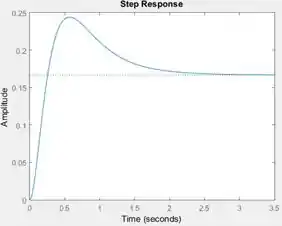
Ao rodar o programa, você terá o gráfico da resposta de a um degrau de amplitude .
Resposta