Plotar a resposta ao impulso de
Passo 1
O exercício pede para gerarmos o gráfico da resposta ao impulso de . Para isto, usaremos a função do MATLAB para criarmos a função de transferência e, em seguida, usaremos a função para ver sua resposta ao impulso.
Contudo, você deve ter reparado que tem um formato um pouco diferente do que estamos acostumados: existe um exponencial no numerador. Um exponencial no numerador de uma função de transferência representa matematicamente um atraso entre o sinal de entrada e o de saída. É uma forma de modelar matematicamente atrasos em sistemas de controle reais. Por exemplo, em um reator químico ou em aeronaves, pode haver uma demora de alguns segundos do sinal de saída, devido a atuadores ou sensores.
Normalmente, funções de transferência que modelam atrasos no sinal tem o seguinte formato:
Onde seria uma função de transferência no formato que estamos acostumados (polinômios no numerador e no denominador) e modela um atraso de segundos entre o sinal de entrada e o sinal de saída.
No exercício, temos segundos e
Veremos que, para incluirmos em uma função de transferência usando o do MATLAB, basta adicionarmos mais uma entrada em indicando o tempo de atraso .
Passo 2
Para entendermos bem como funciona esse conceito de tempo de atraso entre os sinais de entrada e de saída, vamos primeiro trabalhar somente com e ver sua resposta ao impulso.
Usaremos a função para criarmos no MATLAB, que tem a sintaxe:
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
O polinômio do numerador de é . Já o polinômio do denominador é .
No nosso script, vamos criar duas variáveis representando os coeficientes dos polinômios. Como o polinômio do numerador tem somente um elemento correspondendo a , a variável representando seus coeficientes pode ser um número real. Chamaremos essa variável de e ela é igual a .
A outra variável é um vetor chamado , contendo os coeficientes de , indo do elemento com maior expoente () ao de menor expoente (, pois ele multiplica ):
![]()
Tendo criado as entradas de , podemos incluir o comando abaixo para criar a função de transferência :
![]()
A função de transferência é armazenada na variável , isto é, é igual a . Podemos conferir isso rodando o programa e pedindo ao MATLAB para imprimir no Command Window:

Passo 3
Após criarmos , vamos ver sua resposta ao impulso, sem o atraso de segundos, isto é, desconsiderando o componente . A resposta ao impulso de uma função de transferência é calculada usando o comando :
Onde é a função de transferência criada usando o comando . Usando a sintaxe acima, plota-se automaticamente o gráfico da resposta ao impulso de .
Inclua em seu script os comandos:
![]()
Na primeira linha, dizemos que o gráfico que será gerado por será a primeira figura. Incluimos esse comando para que os gráficos sem e com atraso sejam gerados em janelas diferentes e possamos compará-los.
Na segunda linha, usamos a função para vermos a resposta ao impulso de .
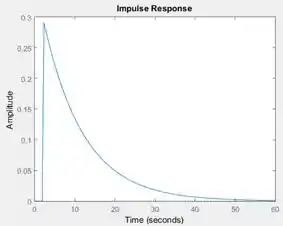
Vamos rodar o programa para vermos a resposta ao impulso sem o atraso de segundos:

Perceba que a curva azul já começa no instante , que é o instante quando ocorre o impulso.
Passo 4
Agora vamos incluir no sistema o atraso de s entre a entrada e a saída, isto é, vamos criar a função de transferência . Lembrando que um atraso entre o sinal de entrada e de saida pode ser modelado assim:
Para modelar um atraso de tempo em uma função de transferência, devemos incluir mais uma entrada na função , que terá o seguinte formato:
Os vetores e contêm os coeficientes dos polinômios do numerador e do denominador de .
Além dos vetores com os coeficientes dos polinômios do numerador e do denominador de , existe uma terceira entrada: . Essa terceira entrada indica que há um atraso de segundos entre o sinal de entrada e o de saída.
Para o exercício, como já criamos e com os coeficientes de no passo 2, para criarmos , vamos só adicionar ao nosso script o comando:
![]()
Com este comando, criamos a função de transferência do enunciado e a armazenamos em . Ao incluirmos como entrada, indicamos que em .
Se você rodar o programa que tem até agora e pedir para ver , você verá que é exatamente a função de transferência do enunciado:

Passo 5
Após criar , vamos ver sua resposta ao impulso. Para isto, adicione em seu script os comandos:
![]()
Na primeira linha, dizemos que o gráfico que será gerado por será a segunda figura. Na segunda linha, usamos a função para vermos a resposta ao impulso de .
Ao executarmos nosso programa, teremos dois gráficos gerados. Você pode colocá-los lado a lado para compará-los:

À esquerda, temos a Figure 1, que tem a resposta ao impulso de , isto é, sem o atraso de s.
À direita, temos a Figure 2, que tem a resposta ao impulso de , isto é, com o atraso de s. Perceba que há uma diferença de em torno de segundos entre as curvas azuis da esquerda e da direita. Isso ocorre devido ao exponencial de , que representa esse tempo de atraso.
Resposta