Uma suspensão automotiva é tipicamente passiva, sendo composta de molas e amortecedores. Para melhorar a suspensão de carros, sistemas de suspensão ativa têm sido propostos. Na figura abaixo, temos um modelo simplificado de uma suspensão automotiva ativa, no qual representa a entrada da superfície da estrada e é a posição vertical do compartimento dos passageiros.

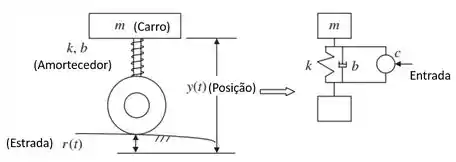
Assuma que a massa do pneu é desprezível e que a velocidade é usada no controle da suspensão ativa. A função de transferência de velocidade da estrada à posição é:

Considere , e . Plote a resposta ao degrau unitário do sistema com e sem controle ativo em um mesmo gráfico. Para considerar o controle ativo, use . Já para modelar o sistema sem o controle ativo, adote .

O primeiro passo é digitar em um script novo os dados , , e :

Note que chamei o valor de para o modelo com suspensão ativa de .

Em seguida, crie um vetor com dois elementos: os valores 0 e . Este vetor vai nos auxiliar a montar dentro do laço :

Inicie um laço , com variável de controle , que vai de a :

Vamos entrar com dentro do laço , escrevendo dentro dele o comando , que tem como sintaxe:

A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .

Vamos criar dois vetores, dentro do laço , contendo os coeficientes dos polinômios do numerador e do denominador de . O polinômio do numerador é e seus coeficientes serão armazenados em um vetor chamado . Já o polinômio do denominador é e seus coeficientes serão armazenados em um vetor chamado . Desta forma, o laço tem essa cara por enquanto:

Logo abaixo dos vetores, já podemos incluir o comando , para criar a variável , que contém .

Note que em vez de eu usar simplesmente , usei , indicando que na iteração vou usar o elemento na posição do vetor . Logo, na primeira iteração, e estará sendo modelada a suspensão sem controle ativo. Na segunda iteração, , sendo modelada, portanto, a suspensão com controle ativo.

Em outras palavras, com o laço de repetição , os vetores e serão atualizados a cada iteração com valores diferentes, gerando, portanto, uma função de transferência diferente a cada iteração.

Para gerar o gráfico com as respostas ao degrau unitário da suspensão com e sem controle ativo, utilize dentro do laço o comando , que tem a sintaxe:

A função plota o gráfico da resposta ao degrau unitário de , que é uma função de transferência criada usando o comando .

Logo, acrescente o comando dentro do laço :

Abaixo de , inclua o comando . Este comando serve para que o gráfico com a resposta ao degrau seja atualizado a cada iteração, mas sem que as curvas da iteração anterior desapareçam.

Pra finalizar, coloque logo abaixo do laço o comando:

Ele fará com que o gráfico com as respostas ao degrau tenham uma legenda, indicando qual curva representa o resultado para a suspensão sem controle ativo e com controle ativo. As legendas dentro de devem estar na ordem com que os diagramas foram criados.

Execute o programa e você terá o gráfico pedido pelo enunciado.