Seja
Plote a resposta de à entrada .
Passo 1
O exercício pede para gerarmos o gráfico da resposta à entrada de uma função exponencial para uma função de transferência . Para isto, usaremos a função para criarmos no MATLAB e, em seguida, usaremos a função , que plota a resposta a uma entrada arbitrária de uma função de transferência.
Como é em função de e o enunciado não especifica mais nada, isso quer dizer que ela foi obtida por meio da transformada de Laplace a partir de funções no domínio de tempo contínuo.
Passo 2
Primeiramente, vamos rever a sintaxe da função :
A função tem como entrada dois vetores, o primeiro contendo os coeficientes do polinômio do numerador da função de transferência (representado por ) e outro contendo os coeficientes do polinômio do denominador (representado por ). retorna um objeto representando a função de transferência, que será armazenada em .
O polinômio do numerador de é . Já o polinômio do denominador é .
Em um novo script, vamos criar dois vetores contendo os coeficientes dos polinômios. O primeiro vetor conterá os coeficientes do polinômio do numerador e será chamado de . O segundo vetor se chamará e terá os coeficientes do polinômio do denominador.
Ambos os vetores vão do elemento com maior expoente ( para o numerador e para o denominador) ao de menor expoente ( para o numerador e para o denominador, pois multiplicam ):
![]()
Tendo criado os vetores de entrada de , podemos incluir o comando abaixo para criar a função de transferência :
![]()
A função de transferência é armazenada na variável , isto é, é igual a . Podemos conferir isso rodando o programa e pedindo ao MATLAB para imprimir no Command Window:

Passo 3
Agora que já entramos com no MATLAB, vamos ver qual é a resposta de à entrada . Para isto, usaremos a função , que tem a sintaxe:
Onde é uma função de transferência criada com ; é um vetor representando uma entrada arbitrária (pode ser qualquer expressão em função do tempo) para cada elemento do vetor , que representa o tempo. O comando , com a sintaxe acima, gera o gráfico da resposta à entrada quando rodamos o programa.
No exercício, queremos ver qual é a resposta para a entrada em função do tempo :
No nosso script, adicione os comandos:

Na primeira linha, criamos o vetor : ele vai de a, com um passo de .
Na segunda linha, calculamos para cada elemento de e armazenamos o resultado no vetor .
Na terceira linha, usamos o comando o para a função de transferência criada no passo anterior.
Ao executar o programa, você terá o gráfico da resposta de a .
Resposta
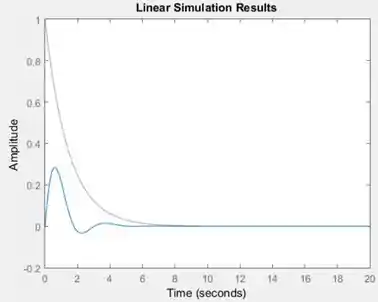
A entrada é representada pela curva vermelha.
A resposta de a é representada pela curva azul.