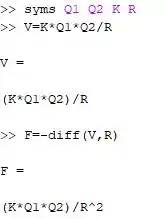Em eletrodinâmica podemos calcular a força entre duas partículas a partir do potencial elétrico utilizando a seguinte expressão:
Utilize a expressão do potencial elétrico para calcular a força entre duas partículas carregadas
Obs: Equação Força é dada por
Passo 1
Fala aí galerinha! O primeiro passo, para fazer uma diferenciação simbólica, é a inserção da função como uma função simbólica. E, para isso, primeiro precisamos introduzir as variáveis simbólicas.
Mas como sabemos que a questão é de variável simbólica? Ou até mesmo quais variáveis são simbólicas?
Bem pessoal, existem diversas formas de deduzir isso, mas a forma mais comum é você perceber que o que a questão está te pedindo é uma expressão.
Em geral, o Matlab gera como saída algum número, então quando a questão te pede uma letra ou uma expressão pode confiar que o problema tem alguma base nas variáveis simbólicas, belezinha?
E para completar precisamos definir quais variáveis são simbólicas né?
As variáveis simbólicas são todas aquelas variáveis pela qual a sua função simbólica depende, ou seja, nessa questão corresponde às variáveis .
Passo 2
Utilizando as informações do passo 1 precisamos implementar as variáveis simbólicas no Matlab, que corresponde a:
Onde a função syms é a função que utilizamos para indicar que as variáveis que vem depois dela é tudo variável simbólica, ok?
consequentemente a função simbólica é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:
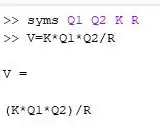
Passo 3
O próximo passo é derivar a função e, para isso, apenas precisamos utilizar a forma padrão da função que vimos na aula. A variável de derivação é o R.
Se você digitou tudo certinho no seu Matlab deve mostrar algo mais ou menos assim:

Resposta