Quando estudamos Mecânica dos materiais vimos de forma aprofundada como calcular a distribuição de força por unidade de área em sistemas deformáveis, uma dessas forças é chamada de tensão de cisalhamento e pode ser calculada para um solido linear pela expressão:
Utilize a seguinte expressão para o cálculo dessa força de cisalhamento:
Passo 1
O primeiro passo como foi visto na teoria é a inserção da função como uma função simbólica. Para isso, primeiro precisamos introduzir as variáveis simbólicas.
Olhando o problema temos que as variáveis são x e y sendo assim:
E a função é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:

Passo 2
O segundo passo é tirar o laplaciano da expressão anterior
Se tudo foi feito certinho, vai aparecer algo assim na sua tela:

Passo 3
Agora que temos as expressões basta integrar em relação a uma variável e depois a outra, logo:
E finalmente ira aparecer a resposta final na sua tela:
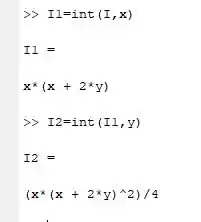
E essa é a função que vai descrever a distribuição de força ao longo de um solido linear deformável.