Em termodinâmica podemos calcular o trabalho da expansão de um gás utilizando a expressão:
Utilize a equação de Estado de Wan der Walls para calcular o trabalho de expansão de um gás de Wan der Walls
Obs: Equação de wan der walls
Passo 1
E aí, pessoal? Tudo bom?
Nessa questão, vamos precisar fazer uma integração simbólica. O primeiro passo é a inserção da função como uma função simbólica. Para isso primeiro precisa introduzir as variáveis simbólicas.
Olhando o problema temos que as variáveis são a, b, V, R e T, sendo assim:
E a função é dada por:
Se tudo foi feito direitinho devemos ter algo do tipo:

Passo 2
O passo 2 é integrar a função e, uma vez que a integral é indefinida, apenas precisamos utilizar a forma padrão da função e a variavel de integração é o V.
No Matlab fica assim:
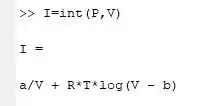
SIIIIIIIIM uma coisa importante o Matlab não conta a constante de integração +C então se estiver fazendo uma prova de cálculo ou algo que precise dele não esquece de somar ela tá?
Daí fica assim: