Listas de Aplicações de Derivadas de Cálculo 1 da UFSC - Lista 3.2 - Taxa de Variação
Cálculo 1 - UFSC
Um fabricante produz peças de tecido. O custo, em reais, da produção de metros de um certo tecido é .
- Qual é o significado de Qual é a unidade de
- O que significa dizer que
A posição de uma partícula sobre uma linha reta graduada em metros no instante segundos é dada por
- Determine
- Determine
- Em quais instantes a partícula está em repouso?
- Quando a partícula está se movendo para frente? E quando está se movendo para trás?
- Qual é o deslocamento da partícula entre os instantes e ?
- Qual é a distância percorrida pela partícula entre os instantes 0 e 5s?
- Para que valores de tem-se Para quais valores de tem-se Para quais valores de tem-se
- Quando a partícula está acelerando ou freando?
A quantidade de carga , em coulombs (C), que passa através de um ponto em um fio até o instante (medido em segundos) é dada por
Em que e são constantes. Determina a corrente neste ponto do fio no instante t. Quais são as unidades de medida?
Ver solução completaA Lei de Gravitação de Newton diz que a intensidade da força exercida por um corpo de massa sobre um corpo de massa é
Em que é a constante gravitacional e é a distância entre os corpos. Calcule e explique seu significado. O que o sinal de menos indica?
Ver solução completaO número de células de levedura em uma cultura de laboratório aumenta rapidamente no início, mas eventualmente estabiliza. A população é modelada pela função
Em que é medido em horas. No instante a população é de 20 células e está crescendo a uma taxa de . Encontre os valores de e . De acordo com este modelo, o que ocorre com a população de levedura depois de muito tempo?
Ver solução completaDois carros iniciam o movimento partindo de um mesmo ponto. Um viaja para o sul a e o outro para oeste a . A que taxa está crescendo a distância entre os carros duas horas depois?
Um carro A está se movimentando para o oeste a 90km/h e o carro B está se movimentando para o norte a 100 km/h. Ambos vão em direção à interseção de duas estradas. A que taxas os carros se aproximam um do outro quando o carro A está a 60 m e o carro B está a 80 m da interseção?
Ver solução completaUm caminhão descarrega areia a uma taxa de de tal forma que a areiai descarregada tem um formato de cone em que a altura é igual ao diâmetro da base. Determine a taxa de crescimento da altura da pilha quando a altura for igual a .
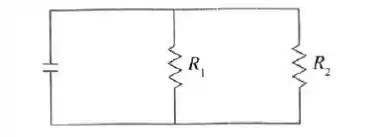
Ver solução completaSe dois resistores com resistências e estão conectados em paralelo, como na figura, então a resistência total , medida em ohms (, é dada por
Se e estão crescendo a taxas de e , respectivamente, quão rápido estará variando quando e ?
Uma quantidade bastante conhecida na Física é o momento, que é dado pelo produto da massa pela velocidade: . A força agindo sobre o objeto é a taxa de variação do momento em relação ao tempo: . Assumindo a massa do objeto como constante, temos , que é a Segunda Lei de Newton. No contexto de mecânica relativística, a massa do objeto não é constante e varia conforme sua velocidade: . Em que é a massa de partícula em repouso e é a velocidade da luz. Usando que e que a massa varia conforme a mecânica relativística, mostre que
Ver solução completaNo estudo de ecossistemas, o modelo predador-presa é muitas vezes usado para estudar a interação entre espécies. Seja o número de tigres de uma região no instante de tempo (medido em anos) e seja o número de antílopes na mesma região no instante . A interação entre essas duas espécies é modelada pelas equações
e ,
Em que e são constantes.
- Como caracterizar matematicamente a afirmação de que o número de indivíduos das duas espécies é constante ao longo do tempo?
- Como caracterizar matematicamente a extinção dos antílopes?
- Considere . Sabendo que as espécies estão convivendo em equilíbrio (isto é, o número de indivíduos é constante ao longo do tempo) e que não estão extintas, determine o número de indivíduos de cada espécie.
É muito comum falarmos em taxa de crescimento usando porcentagens: por exemplo, a população cresce 1% ao ano. Essa medida é uma medida relativa comparada ao seu valor prévio: a população do ano seguinte é 1% maior que a população do ano atual. Apesar de não parecer, essa afirmação pode ser traduzida matematicamente usando a noção de taxa de variação média: se P(t) é a população no ano t, então essa afirmação pode ser escrita como
O denominador da fração do lado esquerdo é , mas colocamos na forma de para ilustrar o quociente que representa a taxa de variação média. E se essa informação da taxa de crescimento relativa não for “média”, mas sim instantânea? Neste caso, o lado esquerdo da igualdade é trocado por e ficamos com
- Mostre que , em que é a população no instante de tempo , é solução da equação acima.
- Mostre que , em que é a população no instante de tempo , é solução da equação .
- Justifique a afirmação: “Em uma população modelada pela função , em que é medido em anos, a taxa de crescimento anual é .”
- Determine a taxa de crescimento anual de uma população que cresce proporcionalmente ao seu tamanho e que, em anos, saltou de bilhões para bilhões de habitantes