Listas de Aplicações de Derivadas de Cálculo 1 da UFSC - Lista 3.6 - Critérios Máximos e Mínimos
Cálculo 1 - UFSC
Defina ponto crítico. Conforme videoaula, dê uma definição diferente que é usada por outros professores e livros.
Ver solução completaDiga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Achar dois números positivos cuja soma seja e cujo produto seja o maior possível.
Ver solução completaUm empresário deseja abrir uma pequena fábrica. Segundo um estudo feito por ele, se funcionários forem contratados, seu lucro anual em reais será de
O estudo considera a possibilidade de contratar até 80 funcionários. Quantos funcionários devem ser contratados para que o lucro anual seja o maior possível? E qual o valor desse lucro?
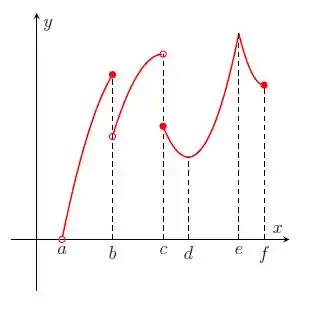
Ver solução completaNos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
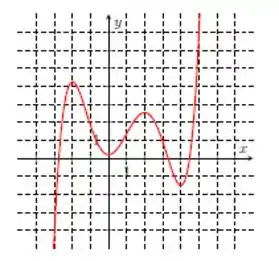
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
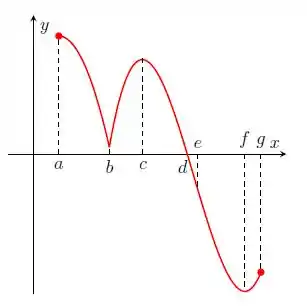
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
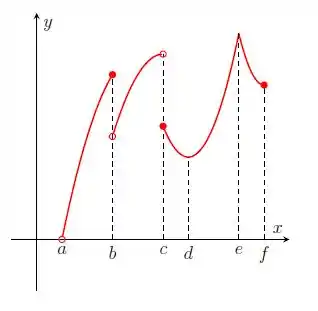
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
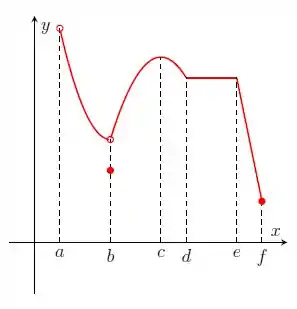
Considere a função . Sabe-se que -3 é ponto crítico e que -16 é valor crítico de . Determine b e c.
Ver solução completaNos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
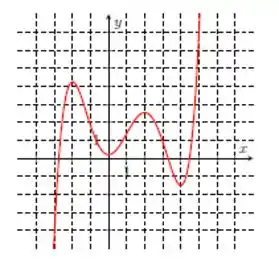
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
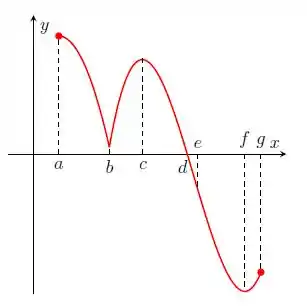
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
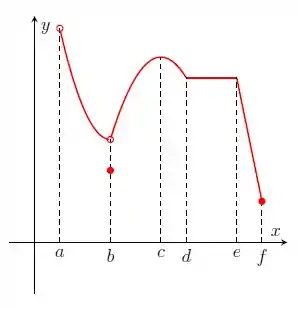
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
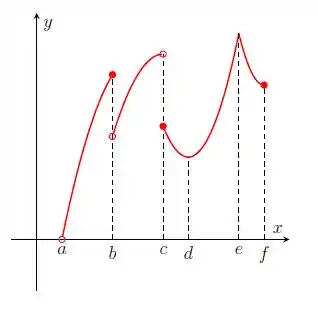
Nos itens abaixo, para a função cujo gráfico é mostrado, identifique todos os pontos críticos, os números críticos e os pontos do domínio nos quais a derivada não existe.
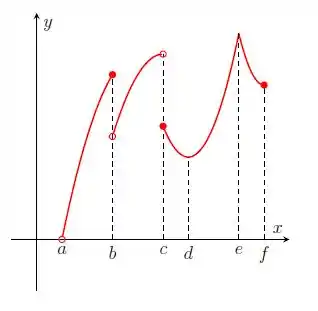
Diga se os itens abaixo são verdadeiros ou falsos. Tente, mesmo que informalmente, justificar suas respostas.
- Todo ponto crítico é um ponto de máximo ou de mínimo local.
- Todo ponto de máxima ou mínimo local é um ponto crítico.
- Todo ponto de máximo absoluto é um ponto crítico.
- Se uma função não possui máximos e mínimos locais então ela não possui pontos críticos.
- Se é um ponto de máximo ou mínimo local e é diferenciável em , então é um ponto crítico.
- Se é um ponto de máximo ou mínimo local, é diferenciável em e é um ponto interior ao domínio de , então é um ponto crítico.
Achar dois números positivos cuja soma seja e cujo produto seja o maior possível.
Ver solução completaUm empresário deseja abrir uma pequena fábrica. Segundo um estudo feito por ele, se funcionários forem contratados, seu lucro anual em reais será de
O estudo considera a possibilidade de contratar até 80 funcionários. Quantos funcionários devem ser contratados para que o lucro anual seja o maior possível? E qual o valor desse lucro?
Ver solução completa