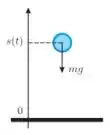
4) Para uma bola arremessada verticalmente sem resistência do ar, temos que a energia mecânica
Se conserva, onde e são, respectivamente, a posição e a velocidade instantâneas, é a massa do bloco e é a gravidade. Supondo que , e que , temos que é a solução da seguinte equação
Como ilustra os itens a seguir, a equação pode ser melhor entendida a partir do fato de que, se a derivada de uma função for identicamente nula em um intervalo, então a função é necessariamente constante.
a) Calcule as derivadas das funções e .
b) Lembrando que se uma função tem derivada identicamente nula em um intervalo , então ela é constante em , use o item anterior e as informações dadas para obter uma relação entre as funções e .
c) Use o item anterior e a condição inicial para obter a expressão de .
d) Determine a velocidade no instante .
Passo 1
Faaaaala, galerinha! Tudo certinho com vocês? Bora lá resolver mais uma questão!!

Começando pelo item a), encontraremos a derivada de em relação ao tempo .
Essa é uma derivada bem simples, não é mesmo?
Já a outra função que precisamos derivar é um pouco mais complexa. Para essa função, temos que usar a regra da cadeia (já que estar em uma raiz torna uma função composta de ) e vamos relembrar que:
Então, para o nosso caso:
Passo 2
No item b), vamos utilizar os nossos cálculos do passo anterior para definir uma relação entre as duas funções.
Pelos cálculos do item anterior e como é a solução da equação:
Daí, temos que:
Para todo tempo . Portanto as funções e diferem por uma constante, ou seja, tem-se que
Onde é uma constante que pertence ao conjunto dos números .
Passo 3
Partindo para o item c), vamos obter a expressão de .
Mais uma vez, usaremos as informações que encontramos no passo anterior para desenvolver o exercício.
Então, usando as informações do item anterior, temos que:
Como (essa informação retiramos do enunciado), obtém-se que:
Agora que conhecemos a constante , podemos aplicar na nossa igualdade encontrada no passo anterior:
Como você já percebeu, vamos resolver a igualdade para encontrar .
Resolvendo:
Continuando a resolução:
Finalizando:
Passo 4
No item d), precisamos definir uma função para a velocidade da bola. Apesar de não termos nenhuma evidência no enunciado do que deve ser feito, vamos utilizar um conceito físico.
A função que definimos foi de , ou seja, de espaço em função de tempo. Se derivarmos essa função uma vez, ou seja, se calcularmos a derivada primeira, teremos a função de velocidade.
Então:
Para finalizar o exercício, encontraremos a velocidade no instante de tempo . Então:
Pra essa questão é isso pessoal! Bora pra mais uma?

Resposta
a) e
b) , com
c)
d)