Lista de Exercícios VE2 de Cálculo 2 da IME - 2019
Cálculo 2 - IME
Seja um campo vetorial irrotacional de classe definido em , onde e . Seja a circunferência de raio 1 centrada em e seja a circunferência de raio centrada em , ambas com sentido anti-horário. Suponha que
- Expresse como uma combinação linear de e com coeficientes racionais, onde é a curva fechada representada no desenho abaixo:
- Supondo que onde
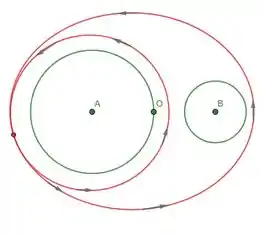
Determine os valores das constantes reais e .
Ver solução completaSeja um campo vetorial irrotacional de classe definido em , onde e . Seja a circunferência de raio 1 centrada em e seja a circunferência de raio centrada em , ambas com sentido anti-horário. Suponha que
- Expresse como uma combinação linear de e com coeficientes racionais, onde é a curva fechada representada no desenho abaixo:
- Supondo que onde
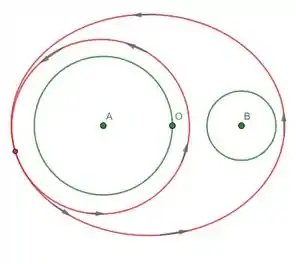
Determine os valores das constantes reais e .
Ver solução completa