Seja um campo vetorial irrotacional de classe definido em , onde e . Seja a circunferência de raio 1 centrada em e seja a circunferência de raio centrada em , ambas com sentido anti-horário. Suponha que
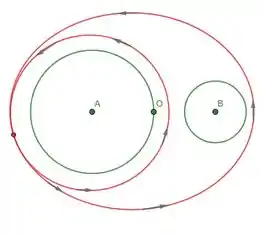
- Expresse como uma combinação linear de e com coeficientes racionais, onde é a curva fechada representada no desenho abaixo:
- Supondo que onde
Determine os valores das constantes reais e .
Passo 1
Fala consagradx! O legal dessa questão é que o desenho é tosco de propósito. Na verdade, campos irrotacionais () são campos gradientes (). Daí,
Esta última condição implica que apresenta invariância segundo deformação de caminhos em . Isto significa que a integral do campo na curva da figura nada mais é que a combinação de deformações das integrais em e (também em ).
Passo 2
Assim, temos que
Pois rodeamos a curva duas vezes no sentido anti-horário e a uma vez no sentido anti-horário