Calcule onde e é a curva de equação , entre os pontos e .
Passo 1
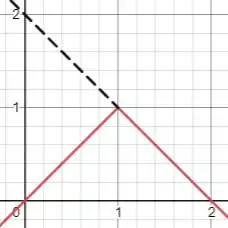
Com
Onde a integral será calculada como:
Passo 2
Com , temos, pois:
Calcule onde e é a curva de equação , entre os pontos e .

Com
Onde a integral será calculada como:
Com , temos, pois: