Listas de Estudos UnB - Cálculo 2 de Cálculo 2 da UnB - Lista 3

01) A temperatura de equilíbrio em um ponto de uma chapa circular feita com um material uniforme pode ser escrita em função das coordenadas polares , de , onde é a distância entre o ponto e a origem e é o ângulo formado entre o eixo e o segmento . Temos que varia em e que varia em , onde é o raio da chapa. Note que o conjunto dos pontos tais que é constante formam uma circunferência.

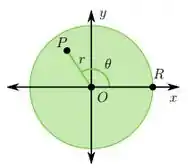
Escrevendo a temperatura em como produto de duas funções , é possível mostrar que as funções e satisfazem as seguintes equações diferenciais:

Onde é uma constante positiva. O objetivo dessa questão é resolver essas duas equações diferenciais e estudar suas soluções.

a) Mostre que satisfaz a equação . Determine os valores de tais que e são soluções fundamentais dessa equação.

b) Use o fato de que e representam o mesmo ponto na chapa, para concluir que . Use esse fato para concluir que , para algum inteiro .

c) Mostre que satisfaz a equação , , conhecida como equação de Euler. Determine os valores de tais que é solução da equação de Euler.

d) Use o item anterior para obter a solução geral da equação de Euler. Verifique que qualquer solução que não é proporcional à solução possui assíntota vertical em .

Considere um elétron no estado fundamental do átomo de hidrogênio, ou seja, no orbital s do primeiro nível de energia, onde e . A probabilidade do elétron estar na região de coordenadas esféricas com , com e com é proporcional a

onde está relacionada com a equação de Legendre

e está relacionada com a equação de Laguerre

O objetivo desse exercício ´eé mostrar que as equações acima sempre possuem uma solução polinomial e qualquer outra solução não proporcional a ela possui assíntota vertical, de modo que, nesse problema, a ´única solução que possui significado físicos é a solução polinomial.

a) Verifique que, substituindo na equação de Legendre, obtemos uma equação linear homogênea de primeira ordem. Determine a solução geral dessa equação.

b) Integrando por frações parciais a solução geral obtida no item anterior, determine a solução geral da equação de Legendre. Verifique que qualquer solução não constante possui assíntotas verticais em 1 e também em .

c) Obtenha o Wronskiano da equação de Laguerre, utilizando a fórmula de Abel e verifique que é solução da equação de Laguerre.

Considere um circuito RLC onde a força eletromotriz é , a resistência é , a indutância é e a capacitância é . Temos que a queda de tensão no indutor, no capacitor e na resistência é dada, respectivamente, por , onde q(t) é a carga no capacitor. A segunda Lei de Kirchoff afirma que a soma das quedas de tensão num circuito é igual à força eletromotriz.

a) Mostre que a carga no capacitor satisfaz uma EDO linear de segunda ordem.

b) Verifique que e são soluções fundamentais da equação homogênea.

c) Obtenha a solução geral da equação não homogênea. A carga no capacitor tende a zero quando t cresce?

d) Determine a carga q(t) do capacitor se a carga inicial é e a corrente inicial é .

Considere um sistema MMA onde a força externa é , a massa é m = 1, a constante da mola é k = 2 e constante de amortecimento é b = 2. Temos que a força da mola e do amortecedor é dada, respectivamente, por ky(t) e by0 (t), onde y(t) é a posição da massa em relação ao equilíbrio. A segunda Lei de Newton afirma que o produto da massa pela aceleração é igual ao somatório das forças.

a) Mostre que a posição da massa satisfaz uma EDO linear de segunda ordem.

b) Verifique que y1(t) = e −t cos(t) e y2(t) = e −t sen(t) são soluções fundamentais da equação homogênea.

c) Obtenha a solução geral da equação não homogênea. A posição da massa tende a zero quando t cresce?

d) Determine uma solução que satisfaz as condições iniciais y(0) = 0 e y’(0) = 1.