Listas de Estudos UnB - Cálculo 2 de Cálculo 2 da UnB - Lista 2

01) Considere um circuito onde a força eletromotriz é uma constante , a capacitância é uma constante e a resistência aumenta linearmente, de modo que . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda Lei de Kirchoff diz que a soma das quedas de tensão em um circuito é igual à força eletromotriz.

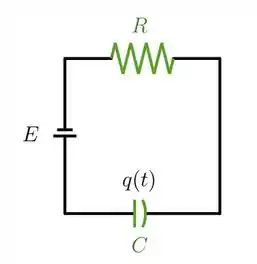
a) Mostre que a carga satisfaz uma equação da forma . Mostre também que a carga constante é uma solução, conhecida como carga estacionária.

Para os próximos itens considere .

b) Encontre uma primitiva de e determine e também .

c) Obtenha a solução geral da equação determinada no primeiro item.

d) Determine a solução com carga inicial . Mostre que, para qualquer carga inicial, após muito tempo decorrido a carga se aproxima da carga estacionária, isto é, mostre que .

02) Considere um circuito RC onde a força eletromotriz é alternada, de modo que , a capacitância é uma constante e a resistência aumenta linearmente, de modo que . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda Lei de Kirchoff diz que a soma das quedas de tensão num circuito é igual à força eletromotriz.

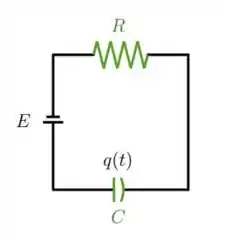
a) Mostre que a carga satisfaz uma equação da forma .

Para os próximos itens considere que .

b) Encontre uma primitiva de e determine e também .

c) Obtenha a solução geral da equação determinada no primeiro item.

d) Determine a solução com carga inicial . Mostre que , mostrando que esse limite não depende da carga inicial .

03) Considere um circuito RC onde a força eletromotriz é uma constante , a capacitância é dada por e a resistência é dada por . Temos que as quedas de tensão no capacitor e na resistência são dadas, respectivamente, por e , onde é a carga no capacitor. A segunda lei de Kirchoff diz que a soma das quedas de tensão num circuito é igual à força eletromotriz.

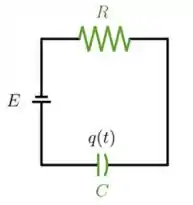
a) Mostre que a carga satisfaz uma equação da forma .

b) Encontre uma primitiva de e determine e também .

c) Obtenha a solução geral da equação determinada no primeiro item.

d) Determine a solução com carga inicial . Mostre que mostrando que esse limite não depende da carga inicial .

04) Num foguete, se o empuxo é uma constante , a taxa de variação de sua massa é constante, de modo que . Se o foguete não atinge uma altura muito elevada, podemos supor que a gravidade é uma constante e que a força de arraste do ar é dada por , proporcional à velocidade do foguete. Segue que a força que atua no foguete é dada por:

Neste caso, a segunda lei de Newton é dada por:

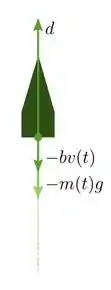
a) Mostre que satisfaz uma equação da forma .

Para os próximos itens considere .

b) Encontre uma primitiva de e determine e também .

c) Obtenha a solução geral da equação determinada no primeiro item.

d) Determine a solução com velocidade inicial . Para que valores de a velocidade está definida?

05) Vamos investigar a dinâmica, num dado país, da relação entre a renda produzida no tempo e o capital acumulado até o tempo através do famoso modelo Solow-Swan. Temos que a renda é dada por uma função Cobb-Douglas do capital e do trabalho, de modo que:

E que o capital se acumula por uma taxa de poupança constante positiva e se deprecia a uma taxa constante positiva , de modo que:

Denotando a renda e o capital per capita, respectivamente, por e por , a taxa de crescimento do trabalho por , a razão riqueza pela renda no tempo por e o seu limite quando tende por infinito por , responda os seguintes itens.

a) Mostre que .

b) Use o item anterior para mostrar que .

c) Mostre que e conclua que

d) Use os itens anteriores para mostrar que

e) Supondo que constante e que , mostre que:

f) Conclua que .