Questão 1: Seja a curva regular dada pela interseção das superfícies

1. Faça um esboço das superfícies e da curva .
2. Descreva uma parametrização regular de .
3. Calcule a integral de linha
4. Calcule a integral de linha

Onde e está orientada saindo do ponto .

Questão 3: Considere o campo e a curva regular por partes onde:

• é o segmento de reta do ponto até o ponto .
• é o arco da parábola de equação do ponto até o ponto .
• é o segmento de reta do ponto até o ponto .

Calcule

Dica: Para aplicar o teorema de Green é necessário fechar a curva. Para facilitar partes das integrais, use a curva que faz com que a região limitada por sua fronteira seja simétrica em relação ao eixo e ao eixo .

Passo 1

Primeiro, para entendermos o problema, acho útil desenharmos a curva:

• é o segmento de reta do ponto até o ponto .
• é o arco da parábola de equação do ponto até o ponto .
• é o segmento de reta do ponto até o ponto .

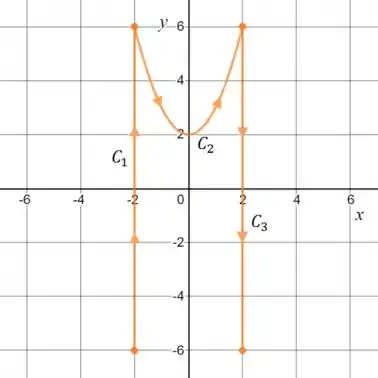
Perceba que a curva é uma composição bem louca, logo, para calcular a integral de linha seria interessante pensarmos no Teorema de Green:

Questão 2: Seja uma função escalar de classe e considere os campos vetoriais

1. Sem calcular potenciais, determinar se e são conservativos;
2. Se conservativos, calcular os potenciais de e ;
3. Seja a circunferência unitária centrada em e o campo vetorial

Calcular