Questão 3: Considere o campo e a curva regular por partes onde:
- é o segmento de reta do ponto até o ponto .
- é o arco da parábola de equação do ponto até o ponto .
- é o segmento de reta do ponto até o ponto .
- é o segmento de reta do ponto até o ponto .
- é o arco da parábola de equação do ponto até o ponto .
- é o segmento de reta do ponto até o ponto .
Calcule
Dica: Para aplicar o teorema de Green é necessário fechar a curva. Para facilitar partes das integrais, use a curva que faz com que a região limitada por sua fronteira seja simétrica em relação ao eixo e ao eixo .
Passo 1
Primeiro, para entendermos o problema, acho útil desenharmos a curva:
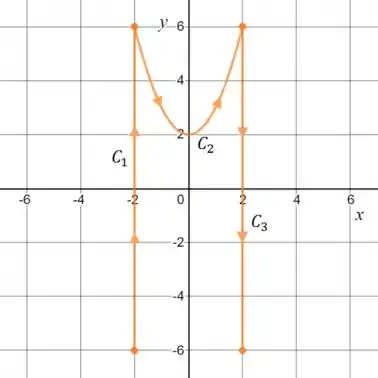
Perceba que a curva é uma composição bem louca, logo, para calcular a integral de linha seria interessante pensarmos no Teorema de Green:
Passo 1
Porém, antes de aplicar essa igualdade para calcular a integral de linha, temos que verificar as hipóteses de Green:
- Primeiro, temos que ter uma curva fechada.
- Segundo, precisamos de uma orientação positiva.
- E por último, não podemos ter singularidades onde estamos trabalhando.
Ora, para começar, a nossa curva é aberta:
Então temos que fecha-la. Mas agora, qual curva é a mais ideal? Ora, para a curva ficar simétrica e facilitar a nossa vida, talvez seja útil uma parábola como essa:
Cuja equação é a simétrica de :
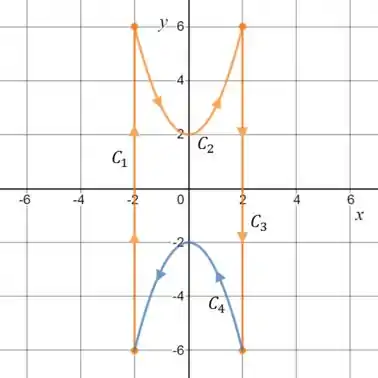
Segundo, temos que verificar a orientação:
Para termos uma orientação positiva, temos que ter a curva girando no sentido anti-horário. No entanto, seguindo a orientação do enunciado, a nossa curva está no sentido horário! Então vamos ter que fazer uma pequena correção. Bom, seguindo em frente!
Por último, não podemos ter singularidades onde estamos trabalhando:
O que acontece perfeitamente, pois o campo não tem algum problema em nenhum lugar algum!
Passo 2
Assim, podemos aplicar a igualdade fazendo apenas uma correção de sinal. A igualdade vale para a curva orientada positivamente. Como ela está no sentido contrário, basta acrescentarmos um sinal negativo em um dos lados da equação:
Mas, a borda é a curva em união com a curva que adicionamos, , logo:
Assim, se quisermos calcular a integral em , basta calcularmos essas duas outras integrais!
Passo 3
Vamos primeiro calcular a integral dupla:
Onde:
Para calcular a integral dupla, ainda precisamos descrever a região :
Podemos descrever a região utilizando a descrição do Tipo , onde o varia entre números:
Logo:
Simplificando...
Passo 4
Agora vamos calcular a integral em :
Temos que calcular do jeito tradicional:
- Parametrizar a curva:
- Calcular o termo :
- Substituir os termos da parametrização:
Logo
Simplificando
Passo 5
Concluímos então que: