2º EE de Física 1 da UFPE - 2017.1

No tempo inicial , uma partícula A de massa parte da posição e move-se em movimento retilíneo uniforme (MRU) com velocidade . No mesmo instante, uma partícula B de massa parte do repouso da posição e move-se em movimento retilíneo uniformemente variado (MRUV) com aceleração . Determine o vetor posição do centro de massa deste sistema de duas partículas no instante .

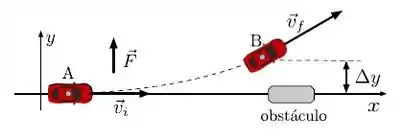
Inicialmente um carro de massa desloca-se na direção com velocidade . Para desviar de um obstáculo aplica-se uma força constante . O carro sofre um deslocamento num intervalo de tempo entre os pontos A e B, conforme indicado na figura abaixo. Escolha o item correspondente ao trabalho realizado por entre os pontos A e B.

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Uma partícula move-se sob a ação de uma única força conservativa, cuja energia potencial associada está representada na figura abaixo.

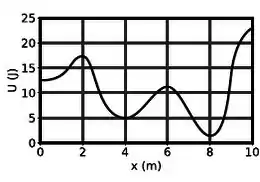
Considerando que num dado instante de tempo a partícula está na posição , com uma energia mecânica total , assinale abaixo a afirmativa que descreve corretamente os pontos de retorno à esquerda e à direita da partícula em metros, respectivamente e :

(a) , e .

(b) , e .

(c) , e .

(d) , e .

(e) indeterminado, e .

(f) indeterminado, e .

(g) Não é possível determinar os pontos de retorno.

Uma bola de massa e velocidade inicial se choca com uma esteira rolante, conforme a figura ao lado. A esteira está em movimento com velocidade para a direita. A bola incide sobre a esteira formando um ângulo , e após a colisão se afasta da superfície formando um ângulo , ambos em relação à normal. Considerando que a bola conserva sua energia cinética, identifique abaixo qual item correspondente ao componente do impulso ao longo da direção , .

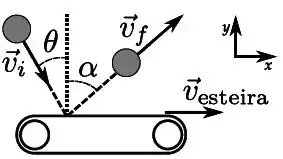
Dados: ; ; ; .

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

(i)

Preencha o campo com sua resposta.

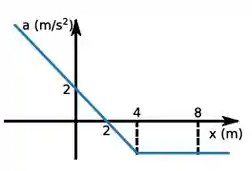
Uma partícula de massa move-se ao longo do eixo . A sua aceleração em função da posição é dada pelo gráfico abaixo. O trabalho da força resultante sobre a partícula entre as posições e é igual a .

Um bloco de massa , sobre um plano inclinado de ângulo está preso por uma corda que passa por uma polia e se conecta a uma mola de constante elástica , como mostra a figura abaixo.

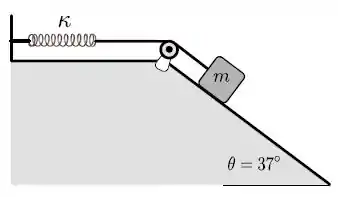
O bloco é liberado a partir do repouso quando a mola encontra-se relaxada em seu comprimento natural. Considere que as massas da corda e da polia, e o atrito no plano e na polia são desprezíveis. Dados:

; ; .

(a) Obtenha a velocidade do bloco após percorrer a distância .

(b) Calcule a maior distância que o bloco percorre sobre o plano antes de parar momentaneamente.

Considere agora que existe atrito entre o bloco e o plano com coeficiente de atrito cinético .

(c) Calcule qual será a nova distância que o bloco percorre sobre o plano antes de parar momentaneamente, neste caso.