Uma partícula move-se sob a ação de uma única força conservativa, cuja energia potencial associada está representada na figura abaixo.
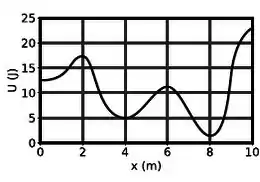
Considerando que num dado instante de tempo a partícula está na posição , com uma energia mecânica total , assinale abaixo a afirmativa que descreve corretamente os pontos de retorno à esquerda e à direita da partícula em metros, respectivamente e :
(a) , e .
(b) , e .
(c) , e .
(d) , e .
(e) indeterminado, e .
(f) indeterminado, e .
(g) Não é possível determinar os pontos de retorno.
Passo 1
Temos um gráfico da energia potencial em função da posição .
Eu sei que o significado desse gráfico pode parecer meio esquisito à primeira vista, mas calma, segura na minha mão e vem!
O que é uma força conservativa mesmo?
Ah é uma força que não retira energia do sistema, ou seja ela apenas faz a energia potencial virar cinética e vice versa.
Po beleza, mas como que sabemos que uma partícula sempre terá aquele determinado valor de energia potencial na determinada posição .
Ah essa explicação é um pouquinho mas profunda, mas a ideia é que realmente essa energia só vai depender da posição na qual a partícula se encontra. Então, realmente conseguimos montar aquele gráfico da energia potencial que uma partícula teria se estivesse na posição .
Okay, falei e falei, mas ainda não entrei na questão.
Passo 2
Agora vem o conceito chave...
Se uma partícula tem uma quantidade de energia mecânica igual a , essa energia mecânica pode transitar na forma de cinética e potencial .
Entretanto, não tem como criar mais energia do que os , ou seja, a partícula não vai conseguir passar de uma posição onde a energia potencial .
Assim, ela estará limitada por essa altura no gráfico:
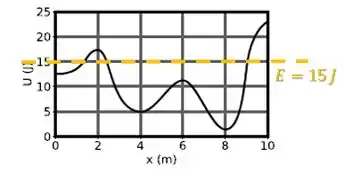
Então, se a partícula parte da posição , ela estará limitada pela esquerda e pela direita pela linha de energia mecânica. Sempre que ela atingir algum dos limites, ela vai parar e retornar, ficando nesse equilíbrio.
Esses pontos onde a particula retorna são chamados de pontos de retorno.

Sim, sério haha.
Então os pontos de retorno à esquerda e à direita serão:
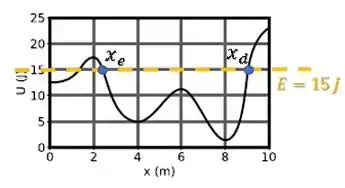
Logo, decobrimos que:
Resposta
Letra (b)