Um bloco de massa , sobre um plano inclinado de ângulo está preso por uma corda que passa por uma polia e se conecta a uma mola de constante elástica , como mostra a figura abaixo.

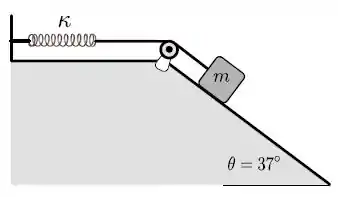
O bloco é liberado a partir do repouso quando a mola encontra-se relaxada em seu comprimento natural. Considere que as massas da corda e da polia, e o atrito no plano e na polia são desprezíveis. Dados:

; ; .

(a) Obtenha a velocidade do bloco após percorrer a distância .

(b) Calcule a maior distância que o bloco percorre sobre o plano antes de parar momentaneamente.

Considere agora que existe atrito entre o bloco e o plano com coeficiente de atrito cinético .

(c) Calcule qual será a nova distância que o bloco percorre sobre o plano antes de parar momentaneamente, neste caso.

Na letra (a), queremos a velocidade do bloco após percorrer uma distância de na rampa.

Podemos pensar em resolver isso calculando a força resultante no bloquinho e vendo sua aceleração, etc...

Entretanto, a força da mola varia a cada instante com uma nova deformação, o que torna as contas um pouco mais complicadas.

Uma boa alternativa é pensar na energia do bloquinho, se a energia se conservar nesse sistema, conseguimos encontrar a energia cinética do bloco e, assim, achar sua velocidade.

Mas será que a energia mecânica se conserva?

Temos três forças atuando no bloquinho, a força peso, normal e de tração:

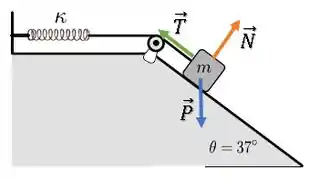
Mas repara que a força de tração, enquanto a corda estiver tensionada, atuará no bloquinho exatamente da mesma maneira que a mola atuaria se estivesse diretamente conectada a ele. Então, vamos considerar que:

E a força normal?

Repara que o movimento do bloquinho é sempre na direção paralela à rampa enquanto a força normal está sempre perpendicular a ela.

Então, o trabalho da força normal será sempre nulo nesse movimento, assim, essa força não retira nenhuma energia do sistema.

Depois dessa análise, vemos que tanto a força peso quanto a força de tração que age como elástica são forças conservativas, ou seja, elas não retiram energia do sistema.

Portanto, a energia mecânica do sistema se conserva sim.

Vamos utilizar a conservação da energia entre o instante inical e o instante onde o bloco andou .

No instante inicial, o bloco está em repouso e a mola relaxada. Logo, temos apenas uma energia potencial gravitacional:

Enquanto no instante final, a mola estará esticada e o bloco apresenta uma certa velocidade. Portanto, se considerarmos o nosso referencial de altura nessa posição, ele terá apenas energia potencial elástica e energia cinética :

Logo, temos:

Okay, já temos todos esses valores, menos a altura do bloco no instante inicial com relação ao instante final.

Para achar a altura, dá uma olhada nesse triângulo aqui:

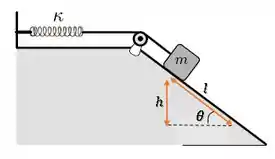
Podemos relacionar a altura que o bloco desceu com a distância que ele percorreu por meio da inclinação da rampa:

Voltando à conservação de energia, temos:

Além disso, a deformação da mola será igual ao deslocamento do bloco :

Achamos a resposta da letra (a).

Na letra (b), queremos saber o quanto o bloco percorreu antes de parar.

Quando o bloco vai descendo a rampa, a mola vai esticando e aumentando sua força, até que em um dado momento, esse bloco vai parar momentaneamente e começar a subir pela ação da mola.

Para descobrirmos o deslocamento máximo do bloco podemos usar a mesma ideia que no item anterior, pois já sabemos que energia no sistema se conserva...

Então vamos usar a conservação de energia entre o instante inicial e final.

No instante inicial, o bloco está em repouso e a mola relaxada, portanto o bloco tem apenas uma energia potencial gravitacional .

Já no instante final, o bloco estará novamente em repouso, porém a mola estarrá esticada, então o bloco terá apenas uma energia potencial elástica .

Assim, temos:

Vamos chamar o deslocamento do bloco novamente de .

Vimos, que a altura com relação ao deslocamento é , enquanto a deformação da mola é o próprio :

Podemos cortar dos dois lados:

Substituindo os valores, temos:

Achamos que o bloco percorre antes de parar momentaneamente.

Na letra (c), queremos a nova distância que o bloco percorre quando considerarmos um atrito entre as superfícies, sendo o coeficiente de atrito cinético .

Agora, a situação mudou um pouco. Como temos essa força de atrito dissipando energia, a energia mecânica do sistema não se conserva mais.

Lembra que o trabalho nada mais é do que a transferência de energia?

Então, o trabalho da força de atrito vai ser exatamente essa energia que sumiu do sistema, ou seja, a diferença entre a energia final e a inical :

Então, bem parecido com o item anterior, temos energia potencial gravitacional no início e energia potencial elástica no final:

Relacionando e com o deslocamento , temos:

Quem vai ser o trabalho da força de atrito ?

Como a força de atrito está agindo contra o movimento, temos que seu trabalho é negativo:

Chamamos o deslocamento de :

Já a força de atrito cinético é dada por:

Então:

Precisamos encontrar a força normal .

Dá uma olhada nas forças no bloco:

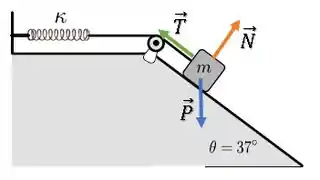
Podemos decompor a força peso em suas componentes paralela e normal à rampa:

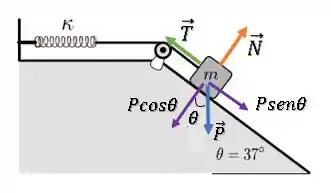
Como o bloco está em equilíbrio na direção perpendicular à rampa, temos:

Voltando à equação de energia, temos:

Cortando dos dois lados:

Substituindo os valores: