Preencha o campo com sua resposta.
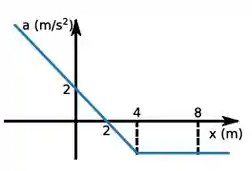
Uma partícula de massa move-se ao longo do eixo . A sua aceleração em função da posição é dada pelo gráfico abaixo. O trabalho da força resultante sobre a partícula entre as posições e é igual a .
Passo 1
Temos o gráfico da aceleração em função da posição e queremos o trabalho da força resultante.
Eita, como a gente relaciona essas coisas?
Vamos começar com o trabalho...
Sabemos que o trabalho é dado pela força média multiplicada pelo deslocamento :
Entretanto, não sabemos o valor médio da força ao longo do deslocamento, então temos que calcular a partir de uma integral:
Onde é a força em cada posição e é um deslocamentozinho que chamamos de infinitesimal.
A integral é apenas um somatório do trabalho realizado em cada deslocamentozinho pelo valor da força que atuava naquela posição.
Até aí okay, mas lembra que temos um gráfico da aceleração e não da força?
Ahhh, então falta um detalhe...
Passo 2
A força aplicada sobre um corpo e a aceleração sofrida por ele são proporcionais. Sabe aquela tal da segunda lei de Newton?
Então, podemos dizer que o valor da força em cada posição é igual à:
Passo 3
Então, podemos calcular o trabalho a partir de:
Agora, já está fazendo mais sentido...
Como a massa é sempre a mesma, ela é uma constante e pode sair da integral:
Além disso, queremos o trabalho em um deslocamento de até . Assim, vamos integrar de até no gráfico:
Vamos calcular isso aí.
Passo 4
A integral de uma função pode ser calculada pela área abaixo do gráfico.
Ou seja, basta nós calcularmos essa área aqui:
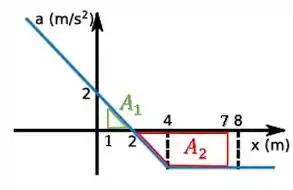
Lembrando que a área acima do eixo (em verde) entra como positiva, e a área abaixo do eixo (em vermelho) entra como negativa.
Então, a integral será:
Vamos calcular cada uma delas, agora.
Passo 5
A área será um triângulo semelhante àquele entre e .
Como sua base vale metade do outro triângulo (base igual a 2), sua altura também será metade da do outro triângulo (altura igual a 2).
Assim, a área será a área de um triângulo de base igual a e altura igual a também:
Já a área é a área de um trapézio:
Onde é a base maior, é a base menor e é a altura.
Além disso, como a reta é simétrica com relação ao eixo , como de a a altura desce unidades, de a , a altura desce mais unidades, então:
A área será:
Então, achamos o valor da nossa integral:
Passo 6
Já calculamos a integral, agora, podemos calcular o trabalho:
Então o trabalho da partícula será de .