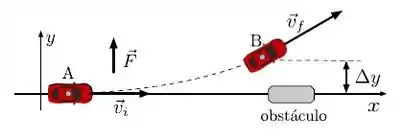
Inicialmente um carro de massa desloca-se na direção com velocidade . Para desviar de um obstáculo aplica-se uma força constante . O carro sofre um deslocamento num intervalo de tempo entre os pontos A e B, conforme indicado na figura abaixo. Escolha o item correspondente ao trabalho realizado por entre os pontos A e B.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Passo 1
Vamos lá, a questão quer o trabalho realizado pela força entre os pontos A e B.
O trabalho de uma força é dado pelo produto interno entre a força e o deslocamento:
O produto interno pode ser escrito como o módulo dos dois vetores vezes o cosseno do ângulo entre eles:
Bla bla bla, o que isso significa?
Isso significa que uma força que está na direção do deslocamento realiza trabalho, enquanto uma força que está perpendicular ao deslocamento não realiza trabalho:
Okay, e daí?
Se na nossa questão, o carro tem tanto um deslocamento na direção do eixo , quanto um deslocamento na direção do eixo :
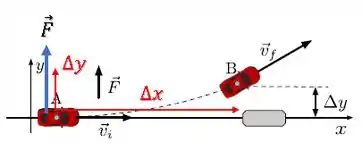
como a força está apenas na direção do eixo , ela realizará trabalho com relação apenas ao deslocamento nessa direção.
Então, o trabalho que buscamos é:
Passo 2
Beleza, já sabemos o valor do deslocamento , porém quem vai ser a força ?
As vezes, viciamos em resolver um exercício por meio de energia e esquecemos de usar aquelas expressões de cinemática (velocidade, deslocamento, aceleração, etc...).
Repara que a força é constante, logo a aceleração também será constante, ou seja, temos um movimento uniformemente acelerado.
Se conseguirmos achar o valor da aceleração, podemos encontrar o valor da força pela segunda lei de Newton:
Passo 3
Então, vamos usar a expressão para um movimento uniformemente acelerado:
Lembrando que estamos analisando apenas a componente em do movimento:
Como o carro, inicialmente, só apresenta velocidade na direção do eixo , sua velocidade inicial em é nula. Além disso, sua posição inicial em também será nula.
Substituindo os valores, temos:
Passo 4
Agora, que achamos a aceleração, podemos achar a força :
Passo 5
Já temos a força, podemos, finalmente, calcular o trabalho:
Podemos, escrever como:
Ficamos com a letra (e).
Resposta
Letra (e)