3º EE de Física 1 da UFPE - 2014.2

A figura mostra um disco homogêneo de raio rolando para baixo sem deslizar, com velocidade angular variável, em uma rampa inclinada em um ângulo . As forças que estão atuando nele são as forças peso , a força normal e a força de atrito . O ponto está no centro de massa do disco. É possível afirmar que:

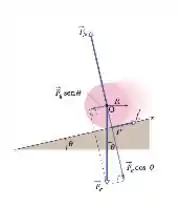
1. Nenhuma das forças mostradas realiza torque em relação ao ponto O.
2. A energia cinética do disco é puramente translacional.
3. A energia cinética total do disco é dada por , onde é seu momento de inércia em relação ao eixo que passa pelo ponto perpendicularmente ao plano do disco.
4. A velocidade linear do ponto do disco em contato com o plano (ponto P na figura) é
5. O torque resultante em relação ao ponto é não nulo e é realizado apenas por .
6. A condição de rolamento sem deslizamento é que o torque resultante em relação ao ponto O seja nulo.
7. A condição de rolamento sem deslizamento é que a aceleração do ponto O seja .

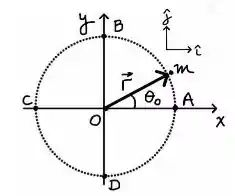
Uma partícula de massa está na ponta de uma haste fina que pode girar em torno de um eixo fixo perpendicular ao plano , passando por sua origem. A partícula pode descrever um movimento circular (linha pontilhada) descrito pelo ângulo com o eixo , orientado positivamente no sentido anti-horário. No instante , a partícula encontra-se parada em (vide figura), quando a haste começa a se mover com aceleração angular constante

Seja o vetor aceleração de , onde e são os vetores unitários nas direções , respectivamente. Quando a partícula passa pelo ponto A pela primeira vez e satisfazem:

1. e
2. e
3. e
4. e
5. e
6. e
7. e
8. e
9. e

Um anel fino de raio e massa é mantido verticalmente apoiado no solo e depois liberado. Suponha que a extremidade de apoio não escorregue. A aceleração gravitacional é . (Dado: momento de inércia de um anel fino de raio e massa em relação a um eixo que passa pelo seu centro de massa paralelo ao seu diâmetro é )

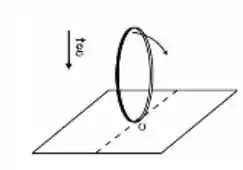
1. Determine o momento de inércia do anel em relação ao ponto de apoio O.
2. Determine a velocidade angular do anel imediatamente antes dele tocar o solo.
3. Determine a velocidade da extremidade mais distante do ponto de apoio imediatamente antes dela tocar o solo.

A figura a seguir ilustra um objeto A composto por duas partículas de massa (cada), fixadas em uma barra sem massa de comprimento 2D . A figura ilustra também uma barra B. O objeto A e a barra B estão sobre uma mesa horizontal sem atrito e têm uma de suas extremidades conectadas, no ponto O, a um eixo vertical, ao redor do qual podem girar livremente. No instante (ver figura) a barra B está em repouso e o objeto A gira com velocidade angular constante no sentido anti-horário. A distância angular entre eles neste instante é .

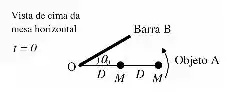
1. Em que instante o objeto A e a barra B colidirão?
2. Calcule o módulo do momento angular do objeto A em relação ao ponto O no instante .
3. Após a colisão, o objeto A e a barra B seguem juntos com velocidade angular . Calcule o momento de inércia da barra B em relação ao eixo vertical passando no ponto O.

Considere o sistema mostrado na figura abaixo. A massa , que desliza sem atrito, está ligada à massa suspensa pelo fio que passa sem deslizar sobre uma polia homongênea de massa e raio . A polia gira sem atrito sobre um eixo horizontal, perpendicular ao plano da polia, que passa por seu centro de massa. A aceleração da gravidade é dada por e o momento de inércia da polia em relação ao eixo mencionado vale . A aceleração da massa , em termos de , , e é: