Um anel fino de raio e massa é mantido verticalmente apoiado no solo e depois liberado. Suponha que a extremidade de apoio não escorregue. A aceleração gravitacional é . (Dado: momento de inércia de um anel fino de raio e massa em relação a um eixo que passa pelo seu centro de massa paralelo ao seu diâmetro é )
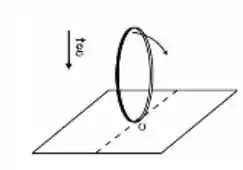
- Determine o momento de inércia do anel em relação ao ponto de apoio O.
- Determine a velocidade angular do anel imediatamente antes dele tocar o solo.
- Determine a velocidade da extremidade mais distante do ponto de apoio imediatamente antes dela tocar o solo.
Passo 1
Beleza! Questãozinha vale 3 pontos, então se errar, a prova começa com 7. Vamos pegar todos os detalhes pra mandar benzão na prova! Bora lá!
Na letra a ele nos pede o momento de inércia do anel em relação ao ponto de apoio O.
Que é mais ou menos isso aqui, oh!
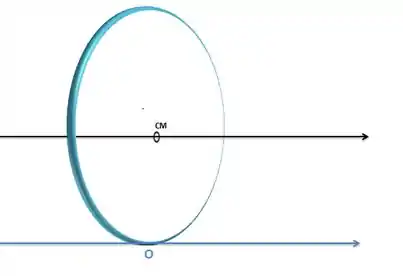
Isso te lembra alguma teorema? Porque me lembrou aqui!
O Teorema dos Eixos Paralelos.
Pra calcular o momento de inércia em um eixo que não é o centro de massa basta usar esse teoremazinho:
a gente quer saber;
ele deu lá no enunciado que é ;
é a massa que é ;
E é a distância entre o eixo que passa pelo CM e o eixo O, que no nosso caso é o raio .
Loogo:
Passo 2
b)
Boy! Só eu achei essa b mal pedida? No enunciado ele fala que estava apoiado no solo e foi liberado . Se estava apoiado ele já tocava, não?
Oo
Mas, enfim!
Pelo que entendi ele quer saber a velocidade angular de quando o anel cai. (Faz mais sentido).
E isso pode ser calculado simplesmente por conservação de energia.
Ele não falou, mas supondo que o anel sai do repouso, e já que o anel vai pro chão.
Assim, teremos:
Lembrando que vamos sempre trabalhar em relação ao centro de massa, a energia potencial, calculada sempre por , vai ser:
Isso porque a altura do centro de massa é .
E como pra o anel cair ele vai só rodar, não vai transladar nada, sua energia cinética pode ser apenas a de rotação, calculada por .
Desta forma, teremos:
Passo 3
O que a gente usa é aquele que calculamos na letra a.
Ouxe, por que?
A gente sempre usa o I em relação ao ponto que está rotacionando. No caso de o anel caindo, o ponto que fica fixo é o ponto O, então temos que usar é o em relação ao ponto O, show?
Logo:
Isolando o , vai ficar:
Passo 4
c)
Num movimento de rotação sem deslizar, como esse aí, temos que:
Na base .
No CM
E no ponto oposto à base
Logo, o meu ali vai ser: