A figura a seguir ilustra um objeto A composto por duas partículas de massa (cada), fixadas em uma barra sem massa de comprimento 2D . A figura ilustra também uma barra B. O objeto A e a barra B estão sobre uma mesa horizontal sem atrito e têm uma de suas extremidades conectadas, no ponto O, a um eixo vertical, ao redor do qual podem girar livremente. No instante (ver figura) a barra B está em repouso e o objeto A gira com velocidade angular constante no sentido anti-horário. A distância angular entre eles neste instante é .
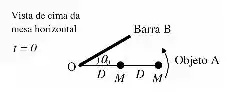
- Em que instante o objeto A e a barra B colidirão?
- Calcule o módulo do momento angular do objeto A em relação ao ponto O no instante .
- Após a colisão, o objeto A e a barra B seguem juntos com velocidade angular . Calcule o momento de inércia da barra B em relação ao eixo vertical passando no ponto O.
Passo 1
Show! Bora lá!
Nessa letra a ele nos pede pra achar o tempo em que eles vão colidir.
Cara, é bem simples.
O enunciado fala que eles estão com um ângulo entre eles e também fala que ele gira com velocidade angular de .
Desta forma, podemos dizer que:
E é só isso! :P
Passo 2
b) O momento angular pode ser calculado por:
O , nesse caso, vai ser calculado por:
Sendo o momento de inercia em relação ao eixo que passa por O das duas bolinhas.
Bora lá!
Loooogo:
Passo 3
c)
Show! Agora temos um caso de colisão com rotação. O princípio básico desse tipo de questão é a conservação do momento angular. Dado por:
Como a barra B parte do repouso, .Daí vai ter:
Como no final eles estarão grudados, e além disso estarão com , teremos:
Arrumando aqui, vai ficar:
a gente já achou lá na B, que é .
Pronto! Agora é só chegar pra mainha e dizer:

(Bode Gaiato- Em Física)